半径の変わる回転体の強制変位を模擬する例題

altair_fukuoka

はじめに

回転体というと、動きを回転角で与えるこちらの記事の方法が簡単です。

https://community.altair.com/discussion/37978/%E5%BC%B7%E5%88%B6%E5%9B%9E%E8%BB%A2%E8%A7%92%E9%80%9F%E5%BA%A6%E3%82%92%E4%B8%8E%E3%81%88%E3%82%8B%E6%96%B9%E6%B3%95

しかしこちらの場合、物体を剛体化してますので、半径が変わることができません。

油圧やアクチュエータ、またはチェーン、ロープの巻き取り、ロック機構などにより、半径を管理できる物体の場合には不向きです。

自由体として半径を強制変位などで管理いたいなら、こちらのように円筒座標系を使う方法があります。

https://community.altair.com/discussion/41265/%E5%BC%B7%E5%88%B6%E5%A4%89%E4%BD%8D-impdisp-%E3%81%A7%E5%86%86%E7%AD%92%E3%81%AE%E5%BE%84%E3%82%92%E5%A4%89%E6%9B%B4%E3%81%99%E3%82%8B%E6%96%B9%E6%B3%95

しかし、半径変わる物体において、周方向の変位を長さで管理するのは、なかなか大変です。それなら、いっそ実験や機構解析で、X,Y,Z 座標履歴を取得して、その X,Y,Z を直接強制変位掛ける方が簡単かもしれません。

やはり、回転体は、半径と回転角で変位を与えるのが、楽なのではないでしょうか？そこで本記事では、周方向の移動は、回転角度で、半径の移動は円筒座標系 R を用いて行う例題を示します。

例題1: 半径が自由に伸縮する物体の強制回転移動

モデルのダウンロード:

kaiten01.7z

今回、白羽の矢を立てたのは、KJOINT2 ばねによるシリンダジョイントです。シリンダジョイントは、名前の通り、軸の回転と軸の伸縮だけできます。もし軸の回転が不要なら、/PROP/KJOINT2, Type=6 並進ジョイントでも良いです。

https://community.altair.com/discussion/41479/%E3%82%B7%E3%83%AA%E3%83%B3%E3%83%80%E3%83%BC%E3%82%B8%E3%83%A7%E3%82%A4%E3%83%B3%E3%83%88%E3%81%AE%E3%83%A2%E3%83%87%E3%83%AA%E3%83%B3%E3%82%B0%E6%96%B9%E6%B3%95

このように、左側のパーツを 180度ぐるんと回します。

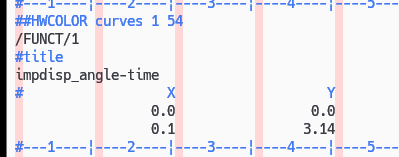
強制変位は、このように回転角度です。

ラジアンのため 3.14=180度です。

このような結果となります。半径方向には剛性がないので、どんどん離れていきます。

半径に円筒座標系で強制変位を与える例題

モデルのダウンロード:

sateliteR.7z

先ほどのモデルに、このように、いったん伸びて、元に戻る強制変位を衛星側に与えます。

円筒座標系を使うため /IMPDISP の Icoor=1 オプションを立てています。

結果です。回転しながら、離れて戻ってくる様子が表現できています。