/MAT/LAW112: 紙、段ボール材料向けの異方性弾塑性材料の例題: ソリッド編
Altair Employee始めに
以前、こちらに、入力パラメータの少ないシェル向けの設定方法を理解するための例題を投稿しました。
今回はソリッド要素向けの設定方法を例題を通して理解していきましょう。シェル編と同じように
- 弾性材料としての設定
- 降伏応力を追加する（応力拡大はまだしない）
- 降伏応力の拡大効果を追加する
という順番でやっていきます。
例題モデルの共通部分の説明
今回は、このように 8 要素用意し、それぞれ異なる試験をします。図内の X,Y,Z は全体座標系です。このモデルは、全体座標系の XYZ が材料方向 123 とそれぞれ同じ向きになっています。
文字で読むよりも、こちらのアニメーションを見る方が、早いでしょう。(変形倍率は 10倍です。)
今回、材料の 13, 23 向きには、同じ特性を入れるため、試験は 13 (XZ) だけ行い 23 (YZ) は行いません。
材料座標系は異方性ソリッドプロパティの中で、座標系 の 2番を与えています。
こちらの定義方法は、こちらの記事を参照してください。
1, 線形材料特性を与える例題
ダウンロード:
/MAT/LAW112 に線形特性を与えるには、次の緑塗の項目を埋めます。
本例題では、このようになっています。
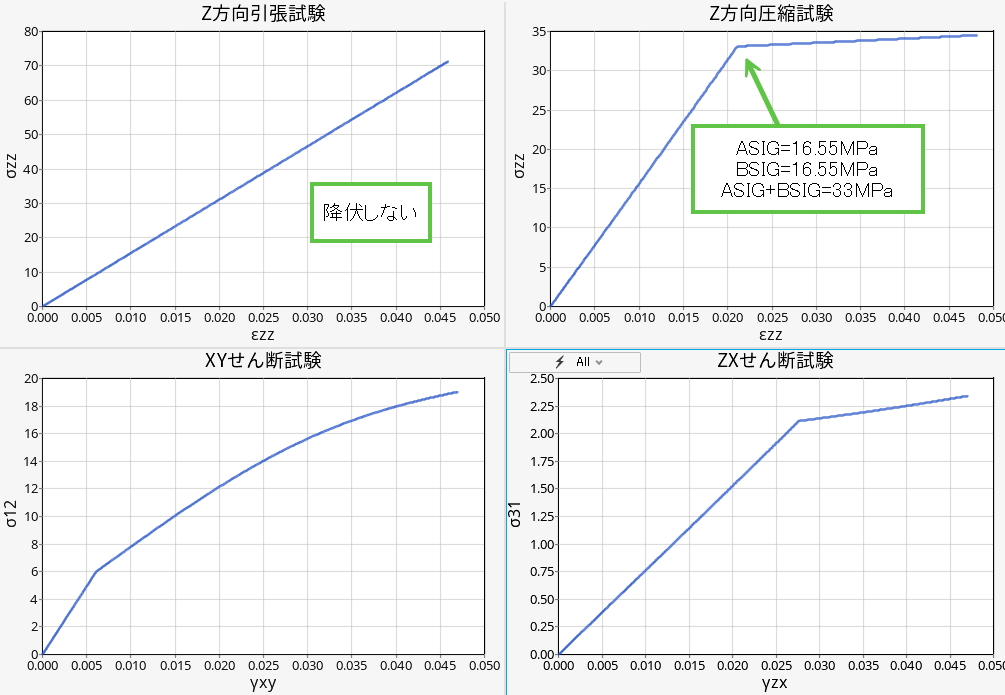
こちらが、応力ーひずみの結果です。試験で変化させている方向の成分にのみ着目しています。また、圧縮側でも、グラフの見やすさを優先して、全て、正の値で描画しています。
指定した傾きがしっかり出ていることがわかります。なお、せん断試験のひずみ γxy は、工学ひずみであり、ひずみテンソル εxy の 2倍としています。σ12=G12 γ12 だからです。γzx についても同様です。
まずはこれで、線形材料をしっかり作ることに成功しました。
2, 初期降伏応力を与える
ダウンロード:
初期降伏応力を与えます。応力拡大の効果は、まだ与えないので、初期降伏応力で応力が頭打ちになります。
入力箇所は次になります。
S01: 材料1 方向、引張の初期降伏応力
S02: 材料2方向、引張の初期降伏応力
S03: 材料方向 12、せん断の初期降伏応力
S04: 材料1 方向、圧縮の初期降伏応力
S05: 材料2 方向、圧縮の初期降伏応力
ASIG: 材料3 方向、圧縮の初期降伏応力
TAU0: 材料方向 13, 23、せん断の初期降伏応力
ASIG は σ33 の圧縮のみ、TAU0 は、τ13, τ23 に対して共通の基準をすることに注意してください。
演習モデルでは、こうなっています。
では応力ーひずみグラフを見てみましょう。
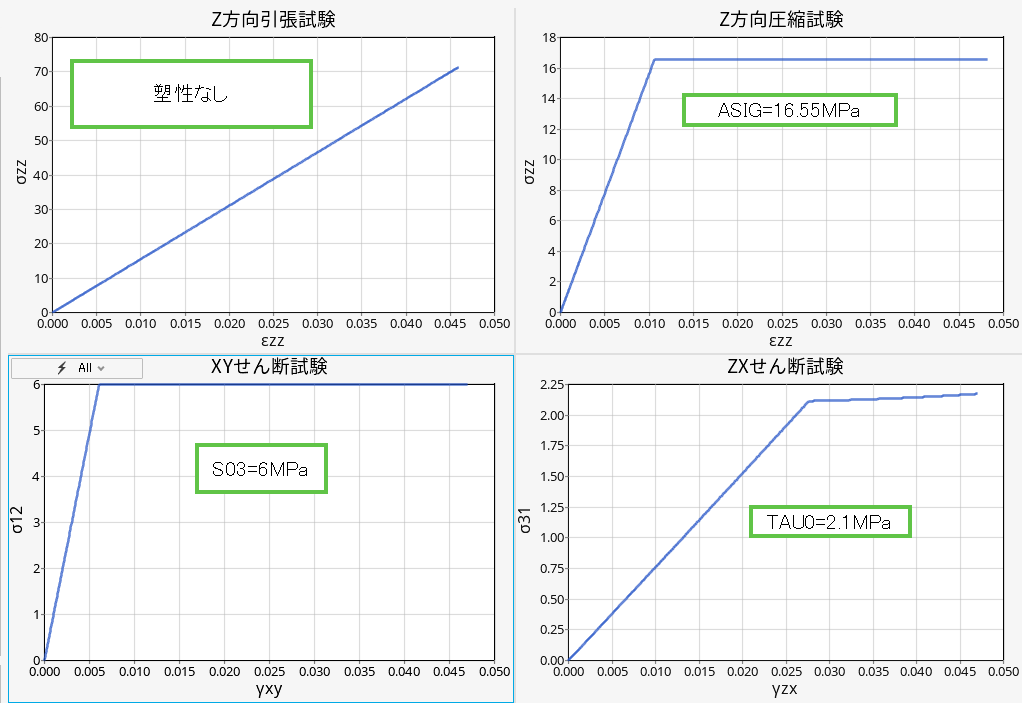
Z 方向引張試験以外は、すべて指定した初期降伏応力で頭打ちしました。Z 方向引張には、降伏の設定がないため、線形材料のままです。
3, 降伏応力を拡大させる
ダウンロード:
必要な入力はここです。
最初の 5行は、面内の応力、σ1, σ2, σ12 に対するもので、次の式が適用されます。
こちらの式の考え方はシェル編で説明したので、そちらを読んでください。
材料 33方向の圧縮にはこちらの式が使われます。
このような２個の項の足し算ですので、圧縮するほど、どんどん降伏応力が大きくなることがわかります。
また exp(0) = 1 ですから、初期降伏応力 σ(εp=0)=ASIG + BSIG と BSIG が上乗せされることにも注目です。
材料 13, 23 の降伏応力は、少しややこしいです。ただ、[] の中身にちゅもくすると、厚さ方向に圧縮を加えるほど (σzz ＜＜＜ 0 となるほど)、[] が大きくなります。
これはダンボールを想像すると分かりやすいかもしれません。段ボールを圧縮していないときは、裏面と表面をずらすことが用意ですが、圧縮してあると、なかなかできない、そういう状況を表現していると考えられます。
本演習モデルでの入力はこちらです。
それでは、SS カーブを見てみましょう。
