始めに
OptiStruct は予荷重または予張力を考慮した固有値の解析ができます。
それを利用して、張り詰めた弦の固有周波数を求めてみます。弦楽器のチューニングと同じです。
長さ L、密度 ρ の弦を、応力 σ で張り詰めたときの固有周波数は、簡単な計算式だと
fn = n/2L √(σ/ρ)
です。単純に、一次の周波数の整数倍となります。
これは、こちらのように、モード内に含まれる波の数から求めるもののようです。
https://wakariyasui.sakura.ne.jp/p/wave/koyuu/genn.html
媒体こそ違いますが、音響管の周波数と同じ考え方のようです。
ということで、はり要素で簡単なモデルを作ってやってみました。
例題
ダウンロード:
例題は単位系を mm, ton, s で作っています。このようなモデルです。
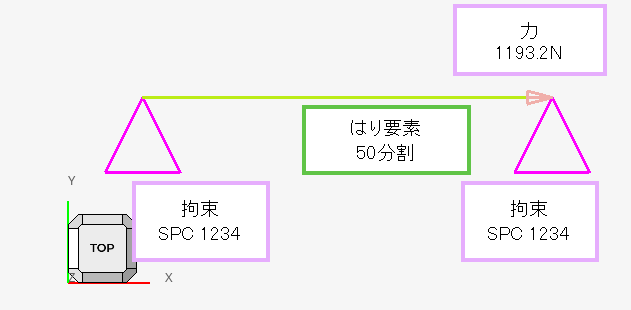
はりの長さは 500mm で、半径 0.5mm の円断面です。
ですので、力を応力に換算すると 1193.2[N] / (3.14*0.5[mm]^2) = 1520N です。
材料は、密度 7.85e-9 ton/mm^3、ヤング率 210000 MPa です。
順番は逆ですが、まず結果から見ていきます。
一次固有周波数は、先ほどの式で 1/2*500*√(1520/7.85e-9) = 440Hz です。
計算すると 440 Hz と整数倍で増えていく固有周波数を得ることができます。次に変形モードを載せますが、y 方向と z 方向に同じ変形モードが出るため、2回同じ周波数が出ています。
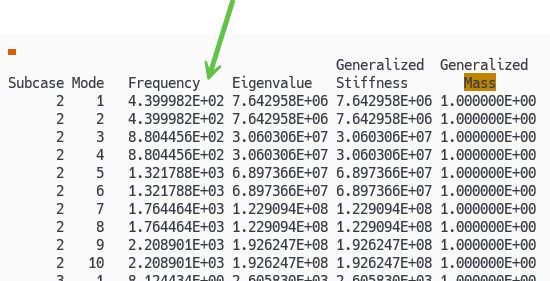
HyperView で見てみると、このようにきれいに波が出ています。

では、OptiStruct の入力ファイルの説明をします。まず、最初のサブケースで、線形静解析をします。そして、次の固有値解析で、STATSUB(PRELOAD) カードを用いて、サブケース 1 を参照します。これで、サブケース1 の応力のかかった状態での、固有値を求めることができます。
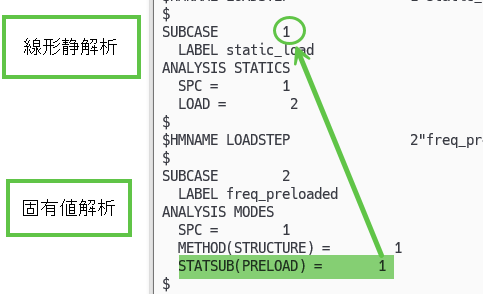
比較用に予荷重を掛けない普通の固有値解析をサブケース 3 に用意してあるので、比較してみてください。