始めに
/MAT/LAW44 は、応力-塑性ひずみの関係はカーブ入力、つまり実験棟で得られた実際の応力と塑性ひずみの値の入力、で行いながら、ひずみ速度依存性は、数式で表現することができるという、変わった材料です。
https://help.altair.com/hwsolvers/rad/topics/solvers/rad/mat_law44_cowper_starter_r.htm
たとえば /MAT/LAW2 の場合、SS カーブもひずみ速度依存もどちらも数式です。
https://help.altair.com/hwsolvers/rad/topics/solvers/rad/mat_law2_plas_johns_starter_r.htm
逆に /MAT/LAW36 の場合、SS カーブもひずみ速度依存もどちらもカーブ入力です。
https://help.altair.com/hwsolvers/rad/topics/solvers/rad/mat_law36_plas_tab_starter_r.htm
現象時間がゆっくりな引張試験の SS カーブは入手しやすいですが、一方で、高速なひずみ速度下での信頼できる SS カーブの入手は難しいと思います。別件で書いた記事ではあるのですが、高速になればなるほど、引張試験片内に均一な1軸引張応力場を作り上げることが難しくなると思うからです。
https://community.altair.com/community/ja?id=kb_article_view&sysparm_article=KB0122424
そうなってくると、信頼できるゆっくりな引張試験の SS カーブと、おおよそこのあたりではないかと目途が付いているひずみ速度依存で、モデルが作れる LAW44 というのは、何かと便利ではないでしょうか。
材料モデルの定義方法
次の図の緑が必須項目、赤は入力してはいけません。入力してしまうと、別のルールが適用されてしまい、本記事の意図である入力方式になりません。

ρi: 密度, E: ヤング率, ν: ポアソン比, fct_IDy: 応力-塑性ひずみカーブ、は良いとして c, p の説明です。
本記事での作り方では、次の式が適用されます。

p の値に関係なく、ひずみ速度 = c となったら応力が 2倍ですから、応力が 2倍になるひずみ速度を c に取ればよいです。

p の値は、大きいほど、ひずみ速度に対して応力が鈍感になり、倍率が 2からあまり変化しなくなります。電卓やエクセルで、ちょうど良い倍率が出るように調整してください。
例
次のような 1要素モデルで実験してみます。一辺 10mm の正方形です。

E= 1000MPa として、応力-塑性ひずみカーブは、倍率を簡単に観測できるように 10MPa 一定としています。
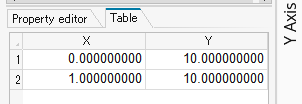
強制速度は、_0000.rad 先頭付近の下図のパラメータを書き換えることで、速度の /FUNCT を書き換えられるようにしてあります (*1)。速度一定ですので、真ひずみで考えると、後半につれてじわじわとひずみ速度が下がることになりますが、大まかな検証には十分です。


そして、c=100 [1/s], p=1.0 としました。

*1) _0001.rad の /RUN, /H3D/DT, /DT, /TFILE などの時間に関する項目はパラメータ化できないので、現象時間に合わせて手で直す必要があります。

ひずみ速度 10.0 [1/s] 相当のとき
期待する応力は 1.1倍、つまり 11MPa あたりです。

しっかり出ています。

ひずみ速度 100.0 [1/2] 相当のとき
期待値はちょうど 2倍です。

こちらもしっかり出ています。

例に使ったモデルのダウンロード
example01.7z
付録1: HyperMesh 2025 での設定動画
HyperMesh 2025 での /MAT/LAW44 設定動画です。
付録2: 速度依存性項のグラフの形
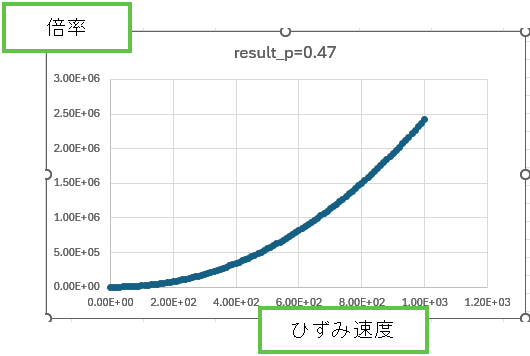
この緑塗の倍率の部分をエクセルで計算してグラフを描いてみました。

C=1 としています。
P=1 は単純な線形です。
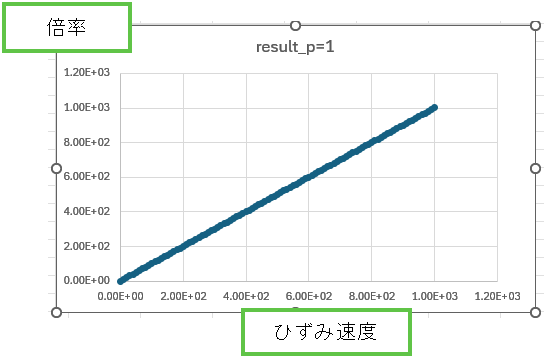
P=0.47 では指数関数的に伸びます。現実的ではないと思いますし、不安定性を導く危険要因でしょう。
P=2.2 では、どんどん伸び悩み続ける形になります。
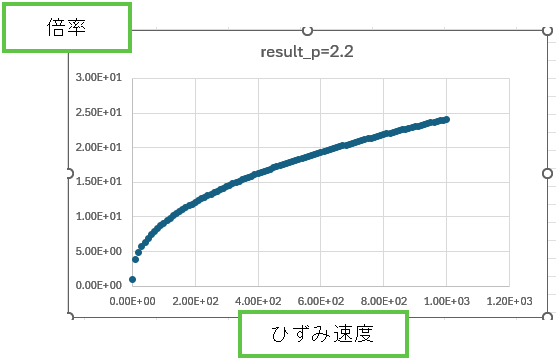
基本的には P>1 で使うものということになります。