始めに
OptiStruct で RBE2 といえば剛体なので、膨らんだり、変形したりするはずがありません。しかし、FEM をやっている、おそらくほとんどの方が、一度は、膨らんだり変形したり、とにかく伸びたり縮んだりする RBE2 というものを体験していると思います。こんな感じで。

本記事では、この例題を示し、なぜこのようなことが起きているのか、説明します。
例題
ダウンロード:
この例題は、赤い RBE2 を 6.28 rad = 360 度回転、つまりまるっと一回転させる条件をつけた、線形静解析です。
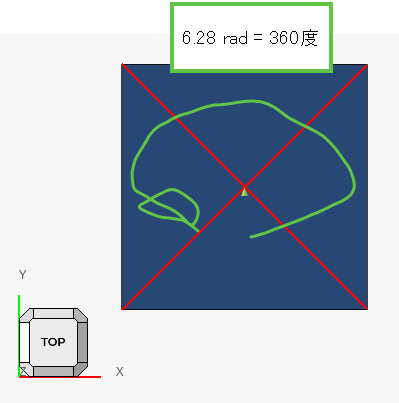
ここで大事なのが、このモデルが「線形」解析であるということです。この事象を OptiStruct で見たことのある方は大勢いると思いますが、(形状非線形解析の) Radioss で見たことがある方は、(ほぼ)ゼロ人だと思います。
「線形」解析が回転をどう扱っているのか、がこの問題を理解する鍵となります。まず、最初のアニメーションを見直してもらいたいのですが、何度見ても絶対に一回転していないですよね。
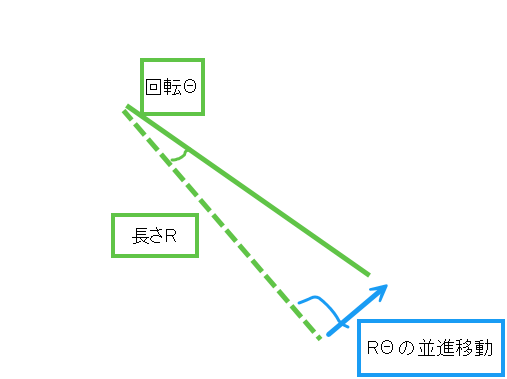
高校や大学の幾何学の内容ですが、下の条件で Θ 動く時の端点の動きは、本来は三角関数やら何やらと、ややこしい式になりますが、Θをぐっと極小化していくと、単純に 90度方向に RΘ 並進することと、と等価になります。「線形」解析は、回転を、この理屈を使い、並進移動として扱います。もちろん極値で成り立つものを、有限の値のものに対して割り当てるので、完全な正解にはなりません。回転量が小さいと非常に良い近似となりますが、大きいと別物になってきます。
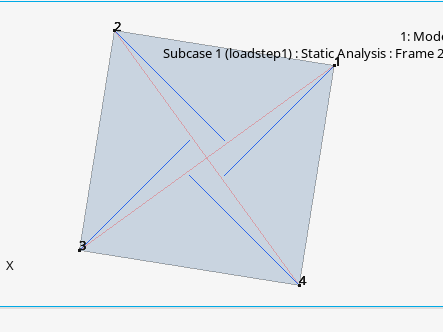
ですので、HyperView で各節点をトレースすると、始めから、まったく回転なんてしていないことがわかります。どの節点も、外に向かって、まっすぐ移動しただけです。
ちなみに 10mm 角の四角形ですので、中心から節点の距離は 5mm x √2。そこに 2π の回転ですから、移動量は 5 x √2 x 2π = 44mm です。
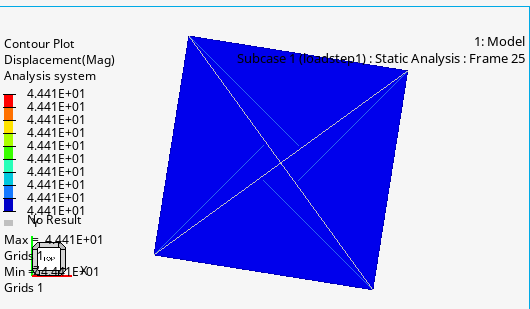
ちゃんとそのようになっています。
これですべてを理解しました。そのうえでもう一度最初のアニメーションを見直してください。私には、最初の出だしだけ、本当に回転しているように見えます。私にはそれが何か面白く感じるのですが皆さまはどうでしょうか?