はじめに
Radioss の接触カード /INTER/TYPExx シリーズや摩擦定義カード /FRICTION の摩擦モデルには Ifric=3 で指定できる Renard 則というものがあり、これを使うと、学校で習った、静摩擦、動摩擦のように滑り速度で変化する摩擦係数を指定することができます。

本記事では、もっとも簡単に、静摩擦、動摩擦として使ってみる方法と、例題モデルを一つ提示します。
簡単な使い方
まず、学校の理科や物理では、静摩擦係数 0.3, 動摩擦係数はその半分の 0.15 などというように習いましたが、このモデルは、そのような 2極化した摩擦係数を取り扱えるわけではなく、あくまでも、滑り速度に対して、なだらかに変化する関数となっています。
その式はこうなっています。

C1 ~ C6 のパラメータですが、最初に結論を書きます。まず、C1 ~ C4 です。
- C3 = 静摩擦係数
- C1 = 静摩擦係数だけど C3 より少し小さくする
- C4 = 動摩擦係数
- C2 = 動摩擦係数だけど C4 より少し大きい
つまり、係数の大きさの順番は C3 > C1 >> C2 > C4 です。
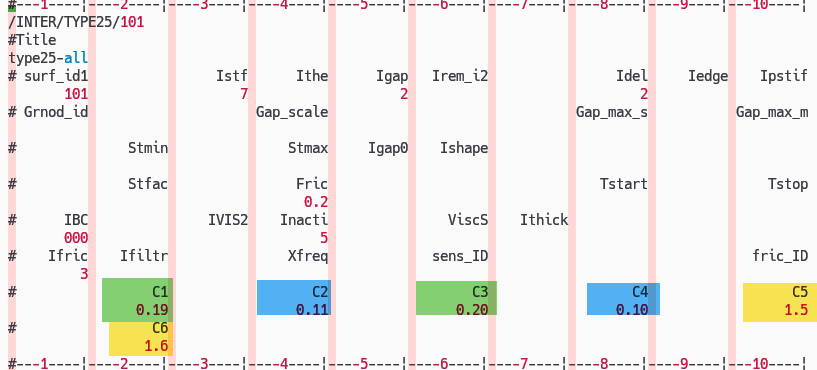
例題では、C3=0.2, C1=0.19,,, C2=0.11, C4=0.1 としています。
C5, C6 は静摩擦から動摩擦に切り替えるときの滑り速度です。C6 を少しだけ C5 より大きくします。例題では、C5=1.5mm/s, C6=1.6mm/s としています。
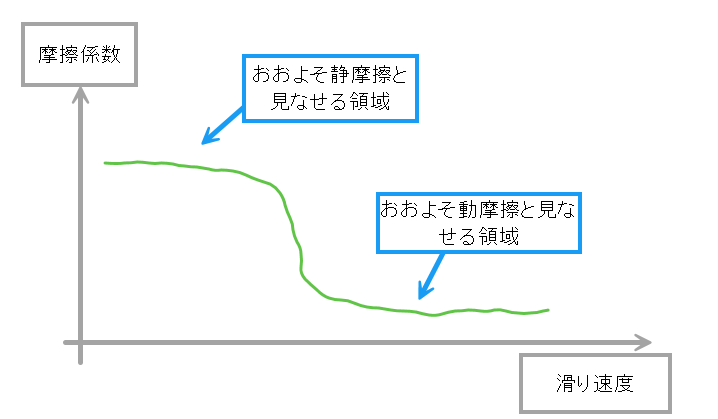
これを踏まえて、最初の式を見ると、滑り速度 V=0 で μ=C1, V=C5 で μ=C3 となります。C1 と C3 をだいたい同じにしておけば V=C5 までは、おおよそ一定の静摩擦状態と言えるようになります。
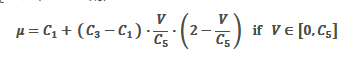
最後の式は、V=∞ にて μ=C2、V=C6 で μ=C4 となり、C2 と C4 をほぼ同じ値にしておけば、V=C6 を超えてからは、おおよそ一定の動摩擦状態となります。
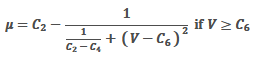
真ん中の式は V=C5 ~ C6 の間の移り変わりの表現ですが、C5 と C6 をほぼ同じ値にしておけば、すとんと移行することになります。
例題
ダウンロード:
モデルはこのようなモデルです。最初の 1秒間押し付けて、次の 1秒でずらします。フォルダが2個ありますが、滑り速度 1mm/s と 2mm/s でずらしたものです。
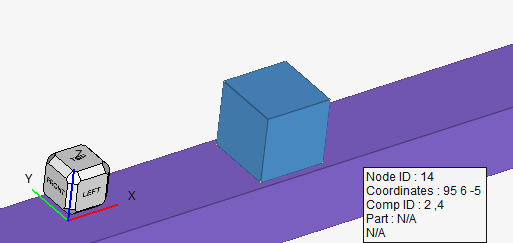
摩擦モデルは、先ほど説明したように、こうなっているので、滑り速度 1mm/s の時は、摩擦係数がおおよそ 0.2, 2mm/s のときは 0.1 くらいになることを想定しています。
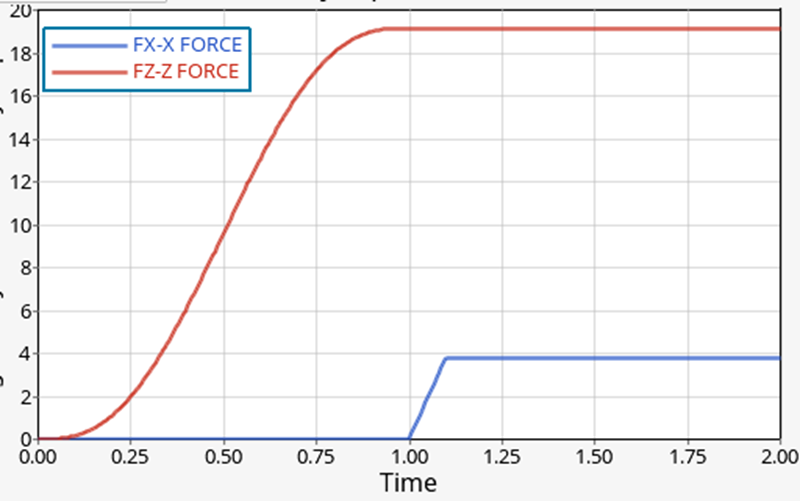
パーツは剛体なので、/TH/RBODY で、負の値とかは見ずらいので絶対値で評価してみました。
こちらは滑り速度 1.0mm/s です。接触力が 19N くらいで摩擦力が 3.8N くらいですので、摩擦係数とすると、おおよそ 0.2 が出ています。
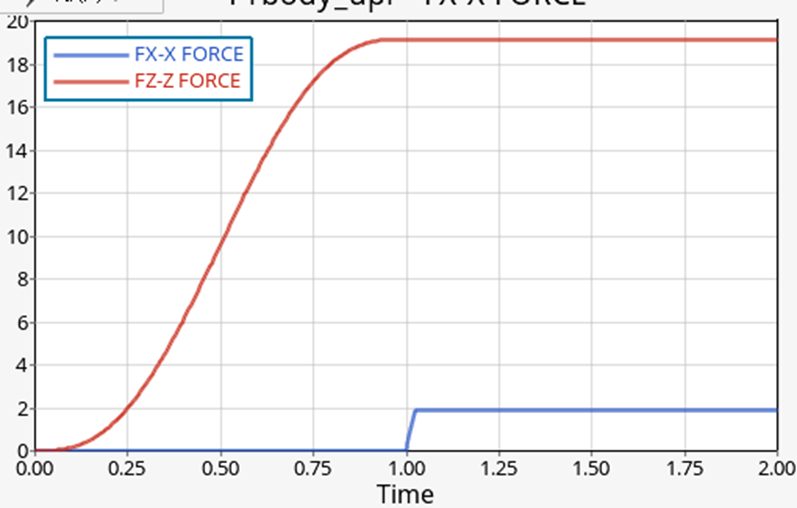
こちらは滑り速度 2.0mm/s です。摩擦力が 1.9N くらいに下がっているので、摩擦係数がおおよそ 0.1 程度となっています。
ということで、静摩擦から動摩擦への切り替えができました。
参考記事
ちなみに、そもそも摩擦の表現がバネなので、学校で習う「静摩擦は全く滑っていない状態」というのは、ある意味条件付きの拘束条件ですので、バネでは再現不可能です。そのあたりを理解するための記事となっています。