テトラ要素 Itetra10=2 と Itetra4=3 を用いた例題
Altair Employee始めに
世の中のほとんどの構造ソルバーには 10節点の 2次テトラと、4節点の 1次テトラがあります。2次テトラは、精度は高いけど、計算コストも高いですし、1次テトラは、計算コストは低いですが、非常に変形が固くなってしまう (特に曲げ、せん断で) ということが知られています。
実は Radioss には、この普通の 2次テトラと 1次テトラの、間に位置するような 2次テトラ (Itetra10=2) と 1次テトラ (Itetra4=3) が用意されています。
本例題では、この２個のオプションを使った、簡単な梁の曲げ問題モデルを提示します。
お題
このような圧力を使った片持ち梁のお題です。
断面のせん断を考慮しない梁理論では、Y 方向のたわみはこのようになります。
P: 圧力 0.3447MPa
w: 断面幅 25.4mm
L: 長さ 508mm
E: ヤング率 193000MPa を使っています
I: 断面二次モーメント = w^4/12 (正方形断面)
ですので、電卓をたたくと 10.9mm です。仮想的な理論とはいえ、さほど外れてはいないと思いますので、11mm くらいたわめば、精度よく計算できていると言えそうです。
比較用に普通の 2次テトラと 1次テトラの例題モデル
普通のテトラを使うときは /PROP/SOLID に何も特別な指定をしなくて良いです。メッシュのオーダーに合わせた普通のテトラが自動的に使われます。
1次テトラ用例題モデル:
2次テトラ用例題モデル:
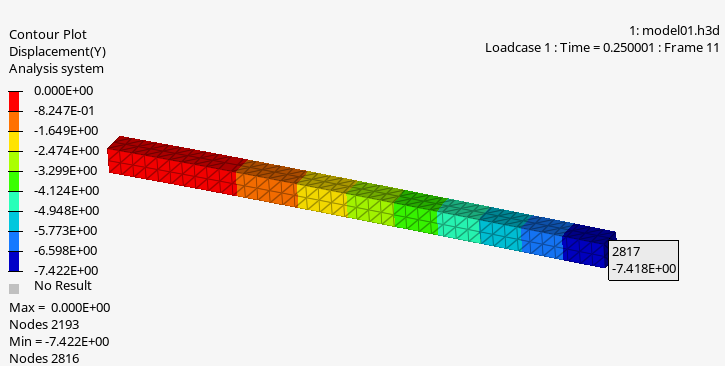
数値は最後に表にしますが、Y 変形量のコンタを載せておきます。2次テトラは良さそうな数値が出ていますが、1次テトラは半分くらいしか変形できていません。
コンタでは分からない計算コストも最後に表にまとめましょう。
Itetra10=2 の 2次テトラの例題
例題モデル:
ここに 2 と入れることで有効になります。
このような説明があり、正直数学的なことは分からないのですが、中間節点を消すけど、おおよそ中間節点があるときと同じような挙動にする (縮退) ことで、節点の間の距離が長くなりますので、その分、時間ステップを稼ごう、という要素です。
変形図です。2次テトラと比べてみてほしいのですが、これくらい単純な計算だと、ほぼどちらがどちらか分からないような結果が得られます。(実際の複雑な形状、接触等の複雑な解析になってくると、それなりに結果に違いは出てきます。あくまで、これは非常に結果が似通る例です)
計算コストについては、最後に表でまとめて比較しましょう。
Itetra4=3, 1次テトラの例題
例題モデル:
ここに 3 を指定します。
こちらは、圧力を要素ではなく、節点で計算するという要素です。応力は要素、圧力(も応力の一種)は節点で計算するという合わせ技の要素なので、ハイブリッド要素などとも呼ばれています。体積ロックというのが、1次テトラ要素の曲げが固くなる要因なのですが、どれほどの効果でしょうか。
普通の 1次テトラが -5.7mm だったので、3割ほど良く曲がったといったところです。
一覧
では変形量とともに、計算時間、サイクル数も表にまとめてみます。小さくて短い計算で ELAPSED TIME (OS の待ち時間などを含めたユーザーが待った時間) がばらついたので CPU 時間を比較してみます。
計算は CPU Intel Xeon Gold 6354 で -np 36 の指定です。この計算にこのような並列数は空回りするだけなので不要なのですが、準備できる環境の関係でこうなっています。
2次テトラが一番精度が良いはずですので (メッシュを細かくしていって、正解＝結果があまり変わらなくなるところを調べれば、この 2次テトラの結果が一番正解に近いはずです。やっていませんが）。
精度、計算コストともに同じ序列です。
精度: 2次テトラ ≧ 2次テトラ Itetra10=2(*1) ＞ 1次テトラ Itetra4=3 > 1次テトラ
計算コスト: 2次テトラ > 2次テトラ Itetra10=2 ＞ 1次テトラ Itetra4=3 > 1次テトラ
そのモデルで、どこを狙うのかを見定めて、一番目的に適したテトラ要素を選んでみてください。
*1) 実際の本番モデルでやってみるとわかりますが、いつもいつも同じ解を得るわけではありません。この問題は、たまたま全く同じになるだけです。