要素の計算（４）古典的アワグラスコントロール
Altair_Ichikawa
New Altair Community Member
有限要素法の定式は、エネルギー最小化に基づいて行われていますので、アワグラスモードのような0エネルギーのモードが存在すると、抑えが効かないことになり、全体の解を壊す原因となります。これに対して、まず80年代に考えられた対処法は、このアワグラスモードを抽出し、その変形に対して粘性または剛性による抵抗を与えようとするものです。これにより、アワグラスモードは0エネルギーモードでは無くなり、自由には変形できなくなります。8節点のソリッド要素を例にとると、1節点3自由度ですので合計24自由度で、各方向に8つのモードが存在します。この内訳は、１つが剛体移動、１つが伸縮変形、2つがせん断変形で、残りの4つが下図のようなアワグラスモードとなります。これらのモードに対して、更にアワグラス以外のモードと直交するように処理を行った上で抵抗を与え、アワグラスモードの発生を抑え込みます。この直交化により、アワグラスモードへの抵抗の付与が他の変形に影響を与えなくする事が出来ます。
現在ではより進んだアワグラスコントロール手法も登場していますが、簡単で、なお有効な手法であることから、今でもRadiossの要素定式化のデフォルトで、粘弾性型の古典的なアワグラスコントロールが用いられています。
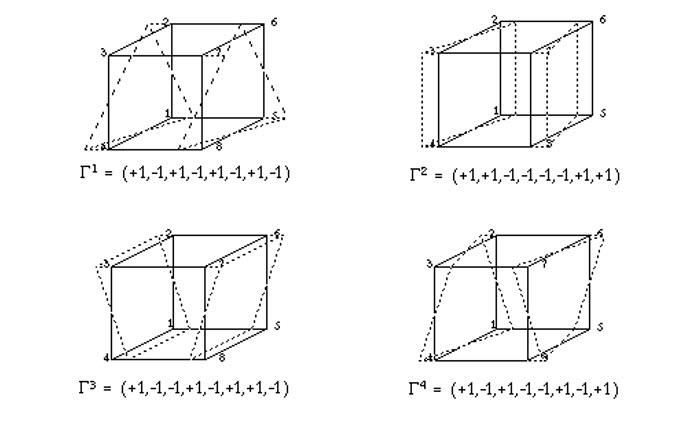
文献：D. P. Flanagan and T. Belytschko, A uniform strain hexahedron and quadrilateral with orthogonal hourglass control Int. J. Numer. Meth. Engrg., 1981, 17, 679-706.
0