要素の計算（１）アイソパラメトリック要素

Altair_Ichikawa

有限要素法では要素毎の計算がいろいろと必要になります。例えば要素の応力から要素節点の節点力を求める、陰解法であれば要素剛性マトリックスを作成する、といった計算です。この計算では、例えばトラス要素であれば節点力は応力σに断面積AをかけてAσ、要素剛性は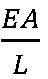といった形で簡単に計算できますが、シェル要素やソリッド要素では要素の面積や体積での積分計算が必要になります。ただ一般の4角形や6面体の複雑な形状で直接計算を行うのは大変なため、一旦、これらの形状を正方形や立方体に写像を行い、定式はその写像された形状に対して行う、といった事が行われます。こうした要素をアイソパラメトリック要素と呼びます。

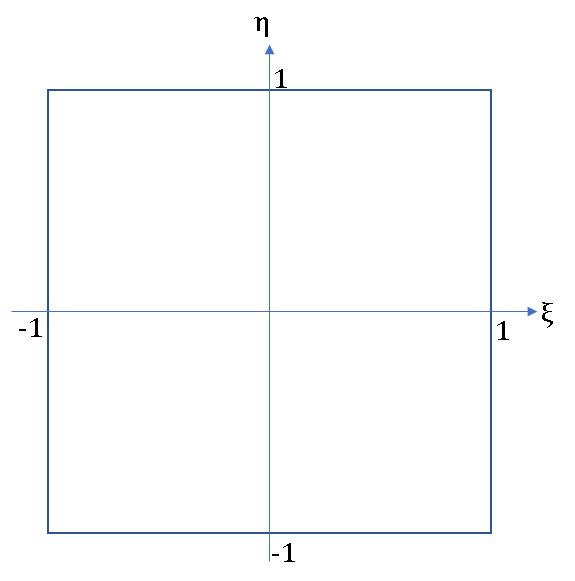
アイソパラメトリック要素では、4角形要素であれば、一旦－1から1の正方形領域に写像を行います。そうすれば、要素面積での積分は

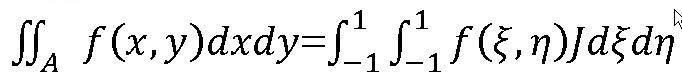 ここに、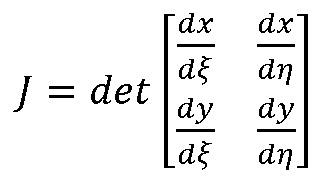

という様に－1から1のξ、η平面での積分に置き換える事が出来ます。この面上での積分には通常、次に述べるGaussの数値積分が用いられます。