Rate-independent Plasticity を分かりやすく説明してみようと思います

altair_fukuoka

非線形材料モデルに、こういう名前のものがあります。rate というのは現象速度のことで、independent ってのは関係ないってことなので、現象速度の効果を考えない塑性ということです。良く分からなければ、単純に塑性ということです。ヘルプに式と出典がありますが、すべての説明がされてるわけでもなく、昔に考えられた式なので出典も入手しずらく、また、同じ理由で日本語の説明も見かけないので、なかなか手ごわいです。自分で行ったテストなどをもとに、なるべく分かりやすく説明して見ます。

 

 

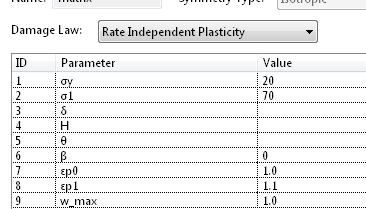
上から順に行くとして、σy, σ1 です。σy は初期の降伏応力で、σ1 は最終的に到達可能な最大の応力です。この２つは、まあ良いでしょう。

 

問題は次の δ です。この δ さえわかれば、なんとなく応力－ひずみカーブを作れますので、この δ だけでも分かりましょう。

 

とりあえず式は、

 

 H(εp) = (σ1-σy) [ 1-exp(-δ εp)]

 

こんなです。H というのが降伏応力の増加量で εp が塑性ひずみなのですが、どういうことなのか、式を考える前に実験から考えましょう。とりあえず、まだ説明してない項目もあるのですが、次の設定で、δ だけ変えていろいろ試してみます。

 

 

 

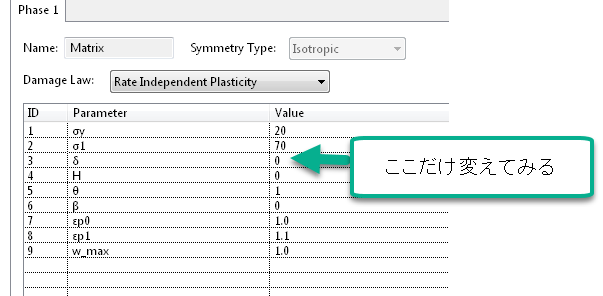
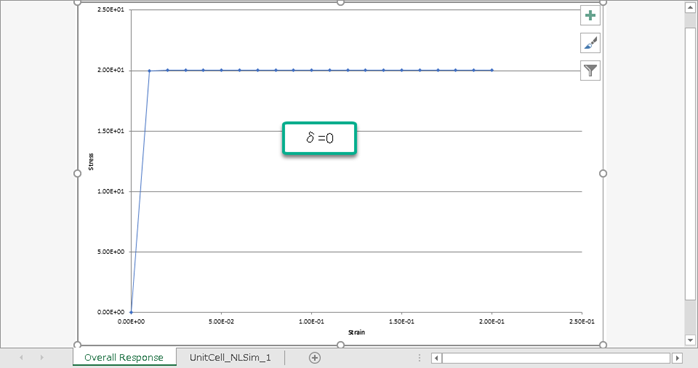
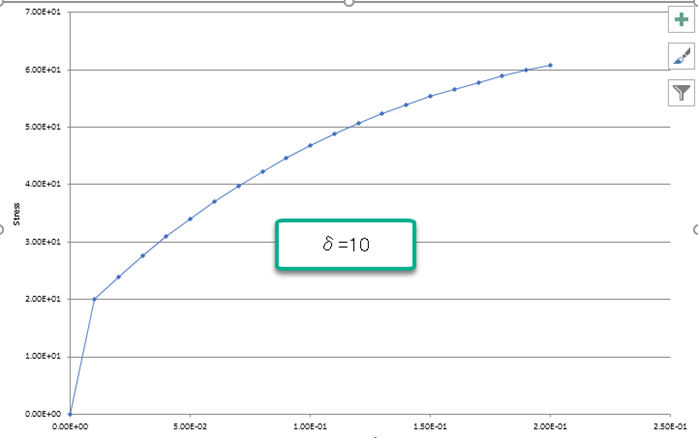
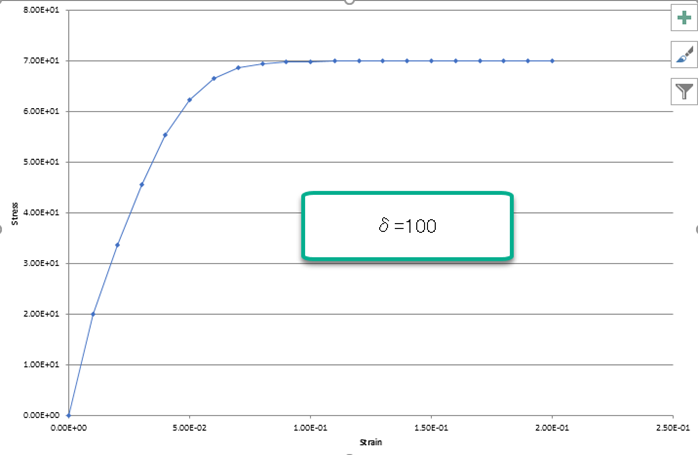
δ を大きくするほど、早く σ1 に到達することが分かります。なるほど、δ は σy から σ1 への到達の早さを調整するパラメータなのですね。あらためて 式をのぞいて見て下さい。δ=0 なら H=0 なのでいつまでたっても降伏応力は増加せず、δ=とても大きい、だと、H(εp=とても小さい)=σ1-σy で、どんどん降伏応力が増加するわけです。

 

どうでしょう、なんとなく形になってきましたね。とりあえず今回はここまでです。