はじめに
OptiStruct のヘルプには様々な例題があるのですが、シンプルに、音響メッシュだけで、音場の、固有周波数 (共鳴の周波数) を計算するものがありません。なにかと、構造―音場連成の周波数応答解析のようになっていたりします。
そういったモデルも、構造の振動解析モデルと、音場の振動解析モデルの組み合わせですので、音場だけの固有値解析モデルの作り方を知っている方が、何かと、そういったモデルを理解する助けにもなると思います。
そこで、本記事では、非常に検証が簡単な、両端を開放した管が作る音場の固有周波数を求めるモデルを提示します。
モデル
ダウンロード:
長さ 220mm, 直径 10mm の管です。全て1次ヘキサ要素ですが、1次テトラ要素でも構いません。

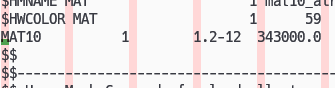
ton, mm, s でモデルを作ったので音響材料 MAT10 は、
- 密度 1.2e-12 ton/mm^3
- 音速 343000 mm/s
としてあります。
ソリッド要素プロパティ PSOLID 自体は構造メッシュの時と同じですが、FCTN=PFLUID とする必要があります。

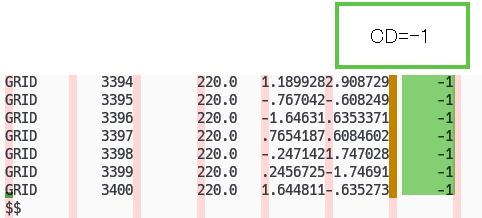
これだけではなく、節点である GRID カードも CD=-1 と入れる必要があります。
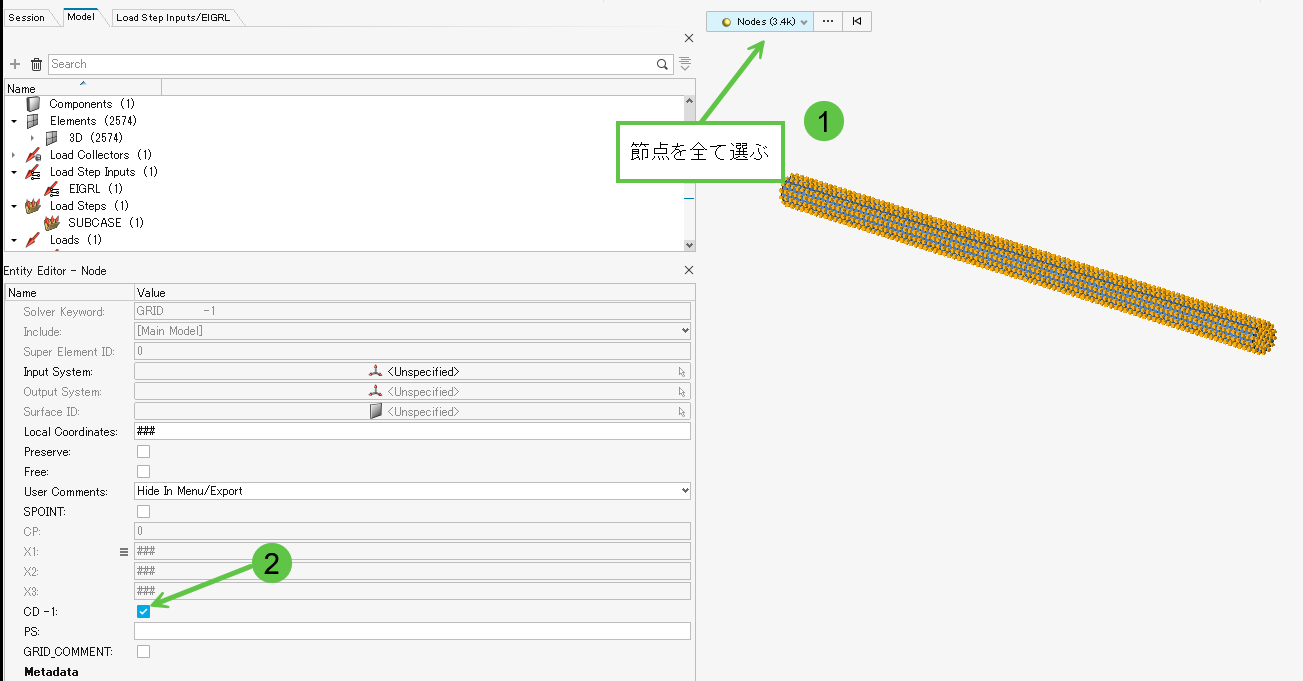
HyperMesh での操作は次のような感じです。
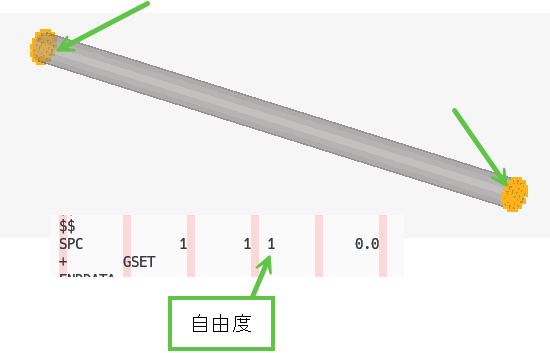
それから、構造解析をやっていると少し不思議な感じがしますが、物理的な壁があるところは、拘束条件は不要です。
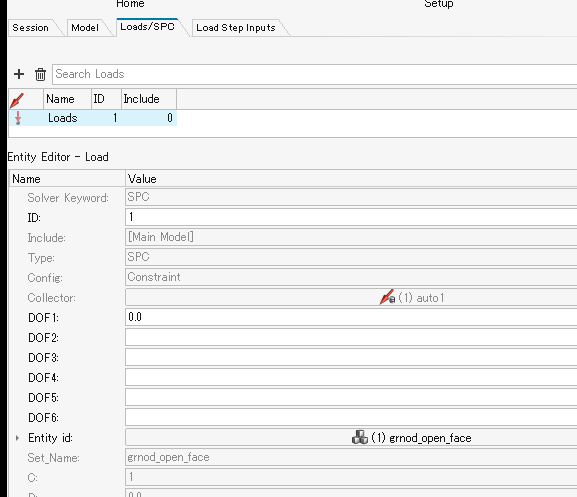
逆に、開放面には、SPC で自由度 1を拘束する必要があります。このモデルでは、次の通りです。ちなみになにを拘束しているのか、と言うと圧力です。頑張って説明を付けると、構造計算では、変位と回転に 6個の自由度がありますが、音響解析では圧力という 1個の自由度しかないために、自由度 C=1 を指定します。
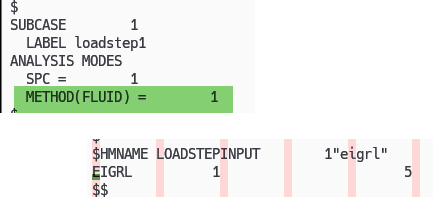
また、固有値抽出条件の EIGRL のサブケース内での参照ですが、構造解析なら METHOD= とか METHOD(STRUCTURE)= となりますが、音響の場合 METHOD(FLUID)= となります。このモデルでは、このようになっています。この例題では 5次まで抽出します。
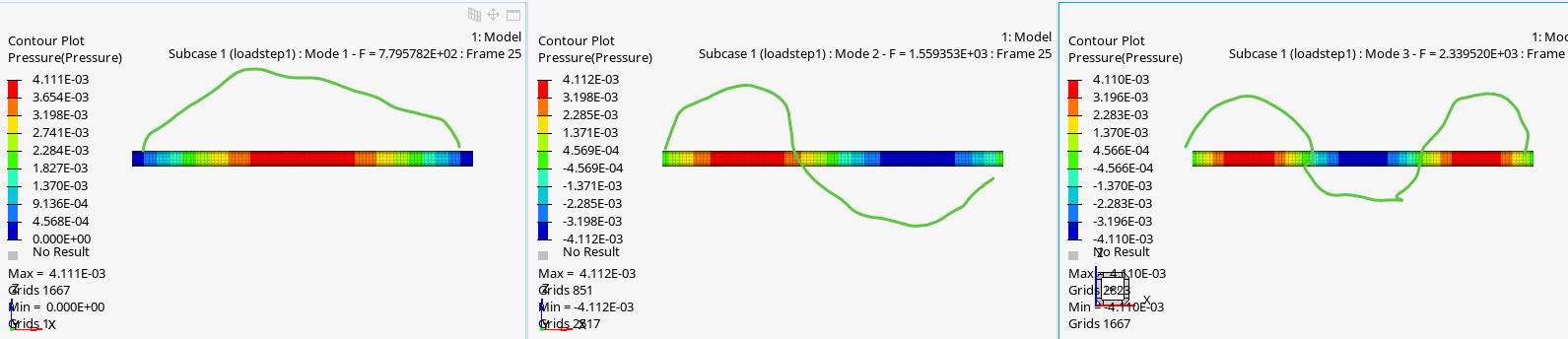
では、.out で結果を見てみましょう。3D 的な効果を無視した理論解は f=nV/2L (V は音速、L=管の長さ)、n が次数なので、1次モードは、780Hz です。大丈夫そうです。

HyperView でも圧力コンタを描かせてみましたが、非常に理論値に近い結果が出ていると思います。
モデル化まとめ
- メッシュはソリッド
- 材料は MAT10
- プロパティは PSOLID に FCTN=PFLUID
- 節点 GRID は CD=-1
- 開放面には、SPC で自由度 1 (圧力) を拘束 (*1)
- EIGRL の SUBCASE からの参照には METHOD(FLUID)=
*) 実験などで測定したインピーダンスを与える方法もあります。今回は、最初の一歩としてもっとも単純なモデルを用意したので、扱っていません。