要素の計算（３）次数低減積分とアワグラスモード
陽解法では、要素の応力分布から要素の節点力（内力）の計算に要素内の積分を必要としますが、これには4角形シェル要素や6面体ソリッド要素では前節で述べたGaussの数値積分が用いられます。実際の積分は応力分布に内挿関数を掛けての積分になりますので、その関数の次数からは各方向に2点の積分点数が必要で、４節点シェル要素であれば面内に2×2=4点の積分点が、6節点ソリッド要素であれば2×2×2=8点の積分点となります。この本来2点の積分点数が関数を正しく評価するために必要なはずの数値積分に対して、これをより少ない1点で済ませてしまう、というのが次数低減積分(reduced integration)です。
陰解法の場合、その計算で最も時間が掛かるのは全体剛性マトリックスの連立一次方程式を解く部分で、計算時間を節約するためには自由度数を減らす事がもっとも有効になります。このため、粗いメッシュでも精度が確保できるように定式は複雑でもより高精度な要素が用いられる事が普通です。
これに対し陽解法では、全体剛性マトリックスを解く必要が無いため、1ステップでの計算量はずっと少なくなりますが、その中での割合を見ると、この要素の計算で全体の3割ぐらいあり、無視できません。そこで、次数低減積分を用いて、シェルでもソリッドでも1積分点での計算で済ましてしまう事ができれば、計算時間の大きな節約になります。
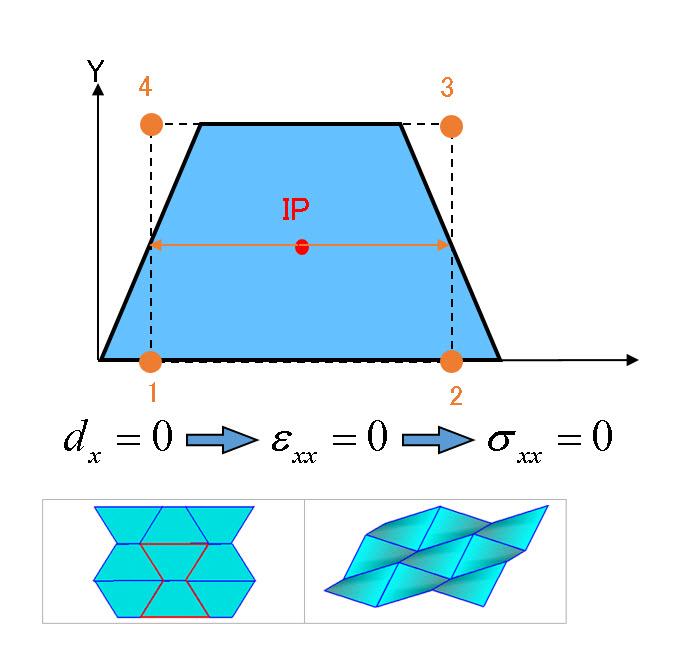
但し、1積分点という事になるとその位置は中央の1点のみですので、例えば、要素が下図の様に台形に変形した場合、要素が変形しているにもかかわらず、中央でのひずみは0で従って応力もエネルギーも0ということが起こり得ます。このようなエネルギー0での変形モードを、要素2つを並べると、丁度、砂時計のような形状となるためアワグラスモード(hourglass mode)と呼ばれます。
