要素の計算（２）Gaussの数値積分

Altair_Ichikawa

－1から1の範囲である関数の積分値を求めるものとして、もし、その関数が1次式であるならば、台形公式を用いるものとすればその積分値はf(－1)+f(1)で得られます(下図参照)。

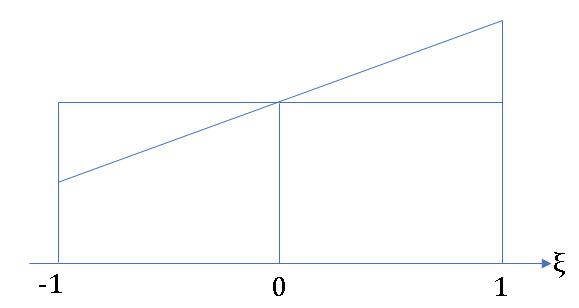
ただ、もしf(0)の値を用いるものとすれば積分値は2f(0)として、１つの点の値だけでその積分を評価できます。Gaussの数値積分は、このように特定の座標(この場合はξ=0)での関数値f(0)と重み(この場合は2)の積で数値的に積分の解を表します。

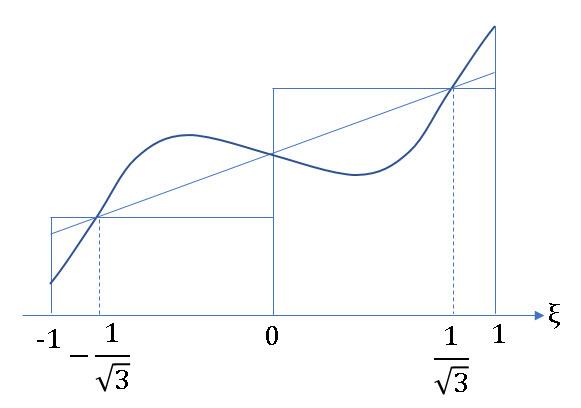
では関数の次数が更に上がった場合にはどうなるでしょうか。例えば下図の様な3次関数を考えると、線と線で囲まれたおのおのの面積を比較すると、3次関数の曲線とξ軸との間の面積、即ち、定積分の値は斜めの直線が作る面積と同じになります。更に、その面積は幅が1で高さがそれぞれ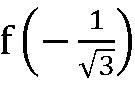と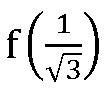の長方形の面積の和になります。図の例に限らず一般論として、2点(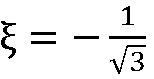と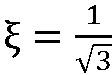)の関数値と重み(それぞれ1)で3次関数の積分値が正確に与えられます。

Gaussの数値積分では、一般にはn点の積分点での値で、2n－1次の関数の積分を正確に与える事が出来ます。