マススケーリング（２）

Altair_Ichikawa

マススケーリングは、時間ステップが小さくなっている節点に質量を付加して最小の時間ステップを大きくする手法ですが、質量が増えれば、当然のことながら、その部分の運動エネルギーが増加し、慣性力も大きくなってしまいます。

このマススケーリングの改良版でアドバンストマススケーリングと呼ばれる手法があります。これは、要素の質量行列において、

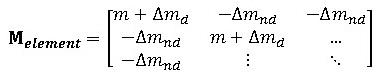　ここに、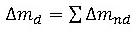

とその対角項にΔm_dを付加するだけでなく、非対角項でΔm_ndを引き算し、全体として、差し引き0とする事で、慣性力の増加をキャンセルしようとするものです。

アドバンストマススケーリングの適用にはEngineファイル(0001.rad)の中で

/DT/AMS

ΔT_sca　ΔT_min

と指定すると共に、Starterファイル(0000.rad)においても、

/AMS

 

と/AMSカードと空行1行を指定します。これでモデル全体にアドバンストマススケーリングが適用されます。ΔT_scaとΔT_minの意味合いについては、通常のマススケーリングと同じです。

アドバンストマススケーリングはすべての問題に対して有効、というわけではありませんが、特にスタンピング解析や、準静的解析では、通常のマススケーリングに比べて10倍以上時間ステップを大きくしても問題ない事が多いようです。但し、アドバンストマススケーリングでは非対角項を持つ質量行列を扱う関係上、1ステップの計算時間が3倍程度に増えますので、それ以上時間ステップを大きくすることが可能な場合には、有効な手段となります。

アドバンストマススケーリングの使い方の詳細については、Radiossユーザーズガイドのアドバンストマススケーリング(AMS)ガイドラインをご覧下さい。Radioss日本語ユーザーズガイドは、Altair Connect：

https://connect.altair.com/CP/downloads.html?suite=HyperWorks

よりダウンロードできます。

また、理論の詳細については下記、参考文献をご参照下さい。

 

文献：Lars Olovsson, Kjell Simonsson and Mattias Unosson: Selective mass scaling for explicit finite element analyses, Int. J. Numer. Meth. Engng., 2005, 63, 1436-1445.