動的応答では、低次の大域的な応答が重要であることが多く、高周波の振動はむしろノイズとして、減衰してくれた方が望ましい事が多くあります。このような目的から、高周波域で減衰特性を持ち、かつその程度をパラメータでコントロール可能な手法として提案されたのがHilber-Hughes-Taylor法です。この方法はNewmark法の拡張として定式化されていますが、減衰特性のコントロールのために新たなパラメータαが導入されていることから、HHT-α法(あるいは単にα法)とも呼ばれます。
Newmark法では、速度、変位が以下のような式で定義されます。
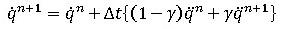 (1)
(1)
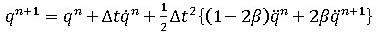 (2)
(2)
モード座標系の運動方程式は、
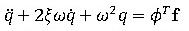 (3)
(3)
ですが、ここでパラメータαを導入し、以下のように表します。
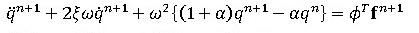 (4)
(4)
簡単のため、外力と減衰を無視すれば、
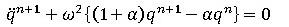 (5)
(5)
式(5)を式(2)に代入して、を消去すれば、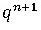 は時刻nだけの値を用いて表せます。同様にして、
は時刻nだけの値を用いて表せます。同様にして、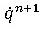 、
、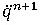 についても求め、まとめると、以下の漸化式を得る事ができます。
についても求め、まとめると、以下の漸化式を得る事ができます。
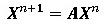 (6a)
(6a)
ここに、
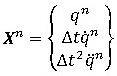 (6b)
(6b)
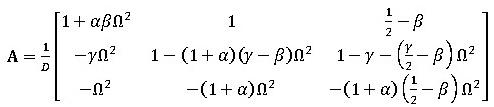 (6c)
(6c)
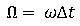 、
、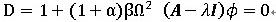
安定条件を満たすためには、式(6)の係数行列Aの固有値の最大値が1以下となる事ですが、固有値問題より、
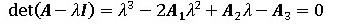 (7a)
(7a)
が得られます。ここに、
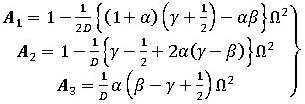 (7b)
(7b)
です。Newmark法では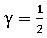 、
、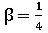 が良く用いられ、この場合前節でも示した通り、無条件安定となりますが、そのスペクトル半径ρはΔtにかかわらず常に1となり、数値的な減衰は生じません。これ以外の値では、
が良く用いられ、この場合前節でも示した通り、無条件安定となりますが、そのスペクトル半径ρはΔtにかかわらず常に1となり、数値的な減衰は生じません。これ以外の値では、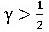 で数値的な減衰が生ずることが知られており、その際、
で数値的な減衰が生ずることが知られており、その際、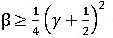 で無条件安定となります。そこで、
で無条件安定となります。そこで、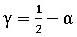 と置けば、
と置けば、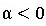 で
で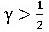 となります。さらにこのγを前述の関係に代入し、
となります。さらにこのγを前述の関係に代入し、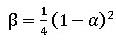 と置けば、パラメータはα一つだけの積分公式とする事ができます。これを式(7b)に代入すると、係数はそれぞれ、
と置けば、パラメータはα一つだけの積分公式とする事ができます。これを式(7b)に代入すると、係数はそれぞれ、
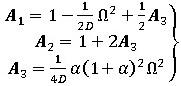 (8)
(8)
となります。式(8)を式(7a)に代入することで次式が得られます。
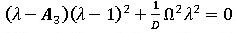 (9)
(9)
Δtが大きくなった場合の安定条件として、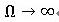 の極限を考えると、式(9)は以下の様になります。
の極限を考えると、式(9)は以下の様になります。
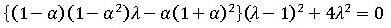 (10)
(10)
ここで、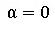 とすれば、。Newmark法(
とすれば、。Newmark法(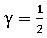 、
、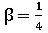 )と一致しますが、そのスペクトル半径
)と一致しますが、そのスペクトル半径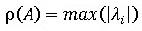 は1となります。αを変化させた場合、
は1となります。αを変化させた場合、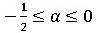 で無条件安定となりますが、
で無条件安定となりますが、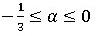 においては、負のαの絶対値が大きくなるほどρは小さくなる(つまり減衰が大きくなる)ため、この範囲でαの値が選択されます。Radioss陰解法(およびOptistruct)でHHT-α法を用いた場合のデフォルトは
においては、負のαの絶対値が大きくなるほどρは小さくなる(つまり減衰が大きくなる)ため、この範囲でαの値が選択されます。Radioss陰解法(およびOptistruct)でHHT-α法を用いた場合のデフォルトは 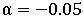 、つまり小さな減衰ですが、αの値を変えることでより大きな数値減衰を与える事もできます。
、つまり小さな減衰ですが、αの値を変えることでより大きな数値減衰を与える事もできます。