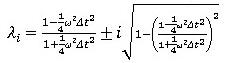時間積分の安定性について （３）Newmark-β法

Altair_Ichikawa

ここでは、陰解法での時間積分公式としてよく用いられるNewmark-β法について見てみましょう。陰解法では、陽解法コードの様に安定限界が問題になることはありませんが、これは時間積分公式にΔtの大きさにかかわらず安定となる無条件安定の積分公式が用いられているためです。無条件安定の公式では、中央差分等を用いた場合と比べ、１ステップ当たりの計算時間もメモリーもずっと大きくなりますが、条件安定という制約条件が外れるために、ずっと大きなΔtで解くことが可能になります。

対象とする運動方程式は、簡単のため、中央差分での検討と同様に、

　

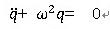
Newmark-β法（γ=1/2 、β=1/4）の変位、速度、加速度の関係式は：

　　 

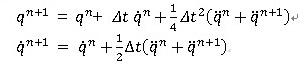
これに、運動方程式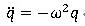を代入すると以下の式が得られます。

　

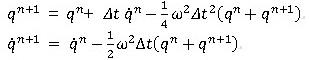
これをまとめて、

　

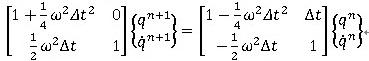
ここで、

　 

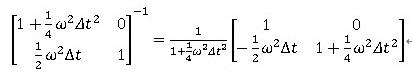
の関係を考慮し、整理すると、

　 　　　 

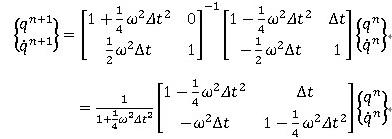
この固有値問題を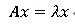考えると、  

　

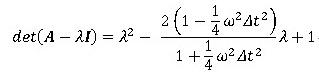
２次方程式の解と係数の関係より、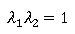であり、もし解が２実根を持つのであれば、１根は常に１より大きい事になりますが、解の公式より得られる根は：

　　

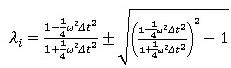
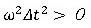より、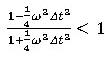である事から、解は常に虚根か重根になる事が解ります。結局：

　

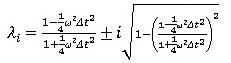
２根の絶対値は：

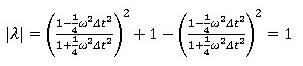
と、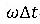の大きさに関わらず１で一定で、無条件安定となります。

<?xml version="1.0" encoding="UTF-8"?>