時間積分の安定性について （１）安定限界
衝撃問題等を陽解法コードで解く際、これ以上Δtを大きくすると解が発散するという限界、いわゆる安定限界がある事が知られています。
これは、Courantの安定条件と呼ばれ、次式で表されます。
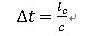
ここに、は要素の代表長さ、cは物質の弾性波速度で、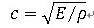
、E:ヤング率、ρ:密度です。これが全ての要素に対して成り立つ必要がありますので、もし、物体の材料が均一ならば、１時間ステップΔtで弾性波が進む距離が最小の要素の長さよりも小さくなるようにする必要がある、というのがこの式の示す所となります。
ところで、数式の解が発散するかどうか、というのは物理の問題ではなく、あくまでも数学の問題です。言ってみれば、Courantの安定条件は、数学的な安定条件の物理的な解釈からなる近似式と言う事ができます。
それでは、数学的な見地から見た場合、この安定条件は、どのように導かれるのかを以下に見ていきたいと思います。
衝撃の問題であれ、振動の問題であれ、その支配方程式は、運動方程式で表す事ができます。
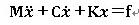
n自由度の運動方程式は、振動のモード解析で知られているように、
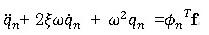
といった、n個のモード座標系での運動方程式の解の重ね合わせで表現できます。このどれか一つでも発散すれば、解は発散することになりますが、その中で一番条件的に厳しいのは、その最大固有振動数の場合ですので、このケースで解が発散しない事を示せれば、安定限界が求められる事になります。
一般に運動方程式を時間方向に解いていく際、その式は、外力等の既知の項を無視すれば、
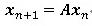
という様な漸化式で表されます、mステップ先まで計算すれば、結局、
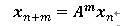
といった計算を行っている事に相当します。この係数行列Aが積分作用素行列と呼ばれます。この行列の固有モードマトリックスをP、その固有値をλと置くと、Aが２×２の行列であれば、
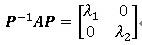
の関係が成り立ちますので、結局、
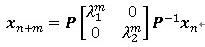
が得られ、mがいくら大きくなっても解が発散しないためには、作用素行列の固有値の絶対値が１を超えない事が必要である事が解ります。即ち、
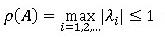
です（ρはスペクトル半径と呼ばれます）。積分作用素行列Aの具体的な形は、用いた時間積分公式によって決まります。陽解法コードでは中央差分法が用いられますので、それによって安定限界が決まり、更にその近似としてCourantの安定条件が得られていた事になります。