タイドインターフェースについて　Type2

Altair_Ichikawa
Altair_Ichikawa New Altair Community Member
edited May 2018 in 質問と回答 (Q&A)

接触条件や結合条件等の拘束条件を表すための方法としては、いくつかの手法があります。例えば、節点1と節点2の変位が等しい、

              u1=u2

という条件を表すためには：

  1. マスター・スレーブ型運動条件

    これは、どちらかの変位(例えばu1)を独立変数とし、もう片方を従属条件、とします。運動方程式を解く際には、u1だけで解き、その後得られたu1をu2に代入すれば、この拘束の条件が、満たされます。つまり、独立節点(マスター節点)だけで先に運動方程式を解き、従属節点(スレーブ節点)は得られたマスター節点の値から拘束条件を満たすように強制的に動かす、と言う方法です。

    かなり乱暴な方法ではありますが、一般に陽解法では時間ステップが非常に小さいため、このような方法でも可能になっています。

  2. ペナルティ法による拘束

    変位の拘束条件：

            u1－u2=0

    に対して、以下の式

            p(u1－u2)^2  / 2

    を考え、これを有限要素法のエネルギー方程式に付帯条件として付加するのがペナルティ法です。pがペナルティパラメータと呼ばれ、これに対して大きな値を与える事で、近似的に変位の拘束条件を満足させます。構造問題の変位の拘束に対して用いられた場合、ペナルティパラメータはばね定数に相当し、変位の拘束条件を満足させる為に、硬いばねで結合した事に相当します。ペナルティ法は近似的な拘束条件ですが、その扱いが簡単なことから陰解法、陽解法を問わず、広く用いられています。

  3. ラグランジュ法による拘束

    変位の拘束条件に対してラグランジュ定数λを導入し、

            λ(u1－u2)

    を有限要素法のエネルギー方程式に付帯条件として付加した上、λでも変分を取るのがラグランジュ定数法です。これは、運動方程式に、拘束の方程式を連立させて解くことに相当します。拘束条件の表し方としては、最も厳密な手法ですが、計算の手間も大きくなることから、主として陰解法で用いられる手法です。但し、Radiossの接触、運動条件にも一部導入されています。

 

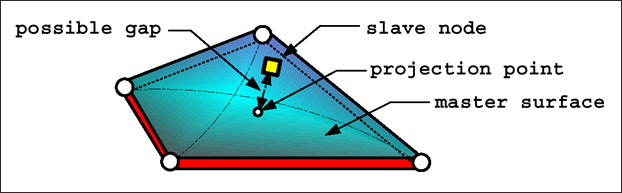
タイドインターフェース(Type2)は、元々節点位置が一致しない異なるメッシュ同士の結合方法として考案されました。ベースになる考え方はマスター・スレーブ型で、マスターセグメントの節点を独立節点(マスター節点)とし、セグメント上のスレーブ節点に掛かった力、モーメントはこのマスター節点に分配した後に、マスター自由度のみで運動方程式を解き、その変形が得られた後、スレーブ節点はマスターセグメント上でのアイソパラメトリック座標が変わらないように強制的に移動されます。

このように、元々は異なるソリッド等のメッシュの結合として生まれたType2インターフェースですが、スポット溶接を模擬するbeam_typeスプリングをメッシュに結合するためにもType2インターフェースが用いられるようになっています。元々のスレーブ節点への力、モーメントのマスター節点への分配が単純分配(spotflag=0)であったのに対して、こちらの手法では、ビームタイプスプリングへの力、モーメントがマスター節点の力と釣り合うように分配されます(spotflag=1)。但し、どちらもマスター・スレーブ型の運動条件ですので、スレーブ節点は従属自由度で、その節点に新たに別の拘束条件が加わると矛盾(運動条件の非適合)が生じます。そこで、この非適合の問題を避けるためType2インターフェースに対してもペナルティ法に基いた拘束(spotflag=0、1に対応してそれぞれ27と28)が導入されています。

<?xml version="1.0" encoding="UTF-8"?>guide_type2-tied.png

Tagged:

Categories