Wouldn’t it be great to be able to run free-size or topology optimization on crash problems? Unfortunately, it is not easy. Traditional topology and free-size optimizations effectively treat each element as a design variable so the gradients with respect to the constraints and objective function must be calculated for each element.
For static finite element models, gradients can be calculated analytically. Crash models are analyzed using explicit finite element solvers which are unable to provide these gradients analytically. This means that the gradients must be calculated using finite difference gradients, which is very computationally expensive.
An approach to save computational effort could be to train a regression model, on which to evaluate these finite differences. However, this would be infeasible for all but the smallest models, as to create even a first order linear regression you would need
Number of Training Points = Number of Design Variables + 1
where each element is a design variable. This would be further exacerbated if interactions or a higher order behaviors were to be considered.
What if we could mitigate this by breaking the link between the design variables and the crash responses? For benign problems this could be achieved by using a linear response to act as a proxy for the crash response, which can then be related to the crash response through a ML model.
For structural problems the most feasible response to act as this proxy would be displacement and its transforms – stiffness and compliance, read this for more information on transforming your data to improve fit quality.
To test the theory that we can relate displacement or stiffness to a crash response, we need to create an OptiStruct linear static model and an equivalent RADIOSS explicit model. Consider the following simple example, a "T" shaped beam which is fully constrained on one end and loaded on the other.
We will evaluate the linear displacement / stiffness by applying a point unit load in the Z direction, and load the explicit model though an impact with a tube that has an an initial velocity. The crash response we will be trying to predict will be the Head Impact Criterion (HIC) ... if you look very closely you will see that the tube is actually a head form!
In order to relate linear displacement/stiffness to HIC, we need to create a Design of Experiments (DoE) in which each evaluation point has a different stiffness, but not necessarily the same deformation mode. To achieve this we can vary the Z position of the nodes on the bottom of the vertical web. This will give us a range of stiffnesses and deformation shapes, eg. a constriction near the support will give a different deformation shape to a constriction near the loading point.
Once we have evaluated our DoE we can compare displacement / stiffness to the HIC response, as shown in the graphs below,
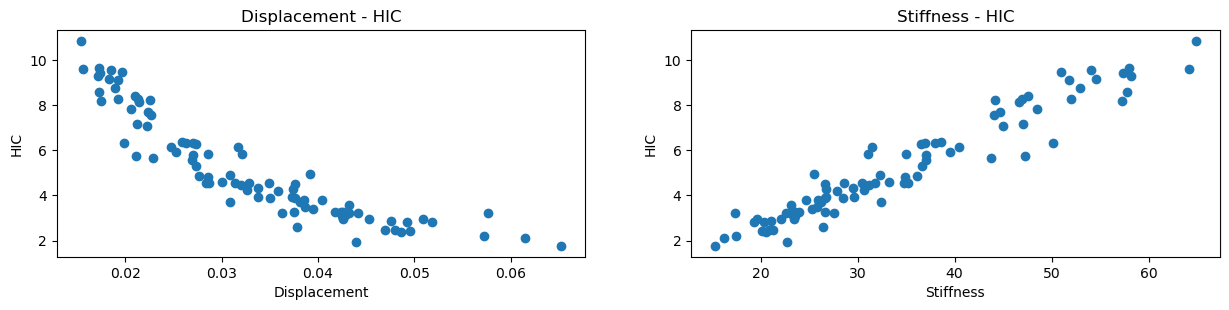
looking at the trends we can see that the Displacement - HIC relationship levels as the displacement increases, but Stiffness - HIC shows a linear trend, thus stiffness is the most suitable feature to use when building a ML model to predict HIC. Using 5 points to create a linear regression model, we get a good quality fit with a R2 of 0.86 as shown below,
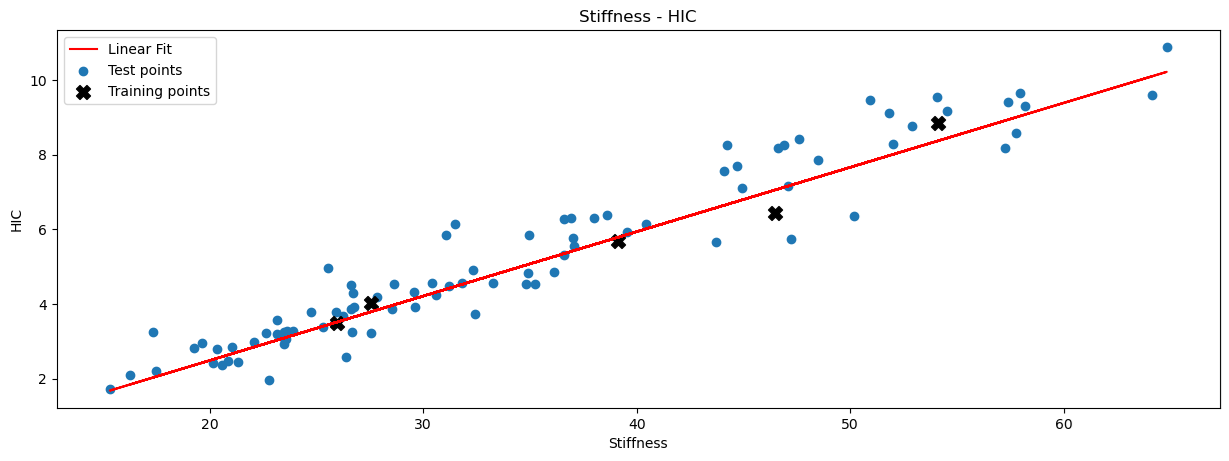
This shows that we can build a good fit using only a small number of training points when using stiffness as a proxy for the design variables. In contrast if we were to take a more traditional approach and build a fit directly from the design variables, for this example, we would need a minimum of 23 training points to build a linear regression model and we would get a worse fit quality with an R2 of only 0.56!
Now that we have a ML model which predicts HIC from a linear response, we can uses it to perform an optimization constraining HIC in one of two ways:
- Derive a stiffness value which will provide the target HIC and use it as a static optimization constraint.
- Reference the ML model in OptiStruct via DRESP3 (read more here) and constrain HIC explicitly.
Using either approach we can optimize for our non-linear response, HIC, within OptiStruct. Calculating the HIC as a function of stiffness provides the prediction with some independence from the design variables, removing the need to calculate gradients of the HIC to the design variables directly. As only the linear stiffness response would be evaluated during the optimization, we could even even perform a topology or free-size optimization.
If the DRESP3 approach were to be taken, a more complex ML model could be used. This more complex model could include other linear finite element responses or model parameters as features, thereby improving accuracy.
This approach will have its limits, it is not likely to be suitable for highly non-linear load cases with large amounts of plasticity or deformation. The stiffness / non-linear response relationship will also need to be calculated on a case by case basis as the relationship and is unlikely to be transferable between models or even loading points on the same model.