Contact stress: Hertz theory vs FEA
Hi everybody,
I'm quite new to the world of analysis involving contact interfaces, so after reading something on the Optistruct help and taking a look at a couple of tutorials, I decided to try to build a FE model for the simple case of a cylinder pressed against a plane, to compare FEA results with the Hertzian theory.
<?xml version="1.0" encoding="UTF-8"?>
Here's a brief summary of the model I built (which you can find attached):
- Cylinder: 50 mm diameter x 100 mm length
- Plane: 200 mm x 100 mm (in-plane size) x 40 mm (thickness)
- Both parts are made of steel (E = 200 GPa, v = 0.3, rho = 7900 kg/m^3)
- All nodes on the lower face of the steel plate are connected through an RBE2 spider to a single node, which is constrained in all 6 DoFs
- A force of 1000 N (applied as pressure) is pushing the cylinder against the plate
- I defined the CONTACT as 'STICK', set ADJUST = 0.0 and DISCRET = S2S, Slave surface is the cylinder and Master surface is the plate
(Despite what I've written above to describe the model, all units used are consistent: length [m], pressure [Pa], density [kg/m^3])
Unfortunately, analysis results are not even close to what the Hertzian theory predicts (I used as reference: https://amesweb.info/HertzianContact/HertzianContact.aspx), as you can see from the following pictures (maximum contact pressure: predicted 118.3 MPa, calculated 3.11 MPa).
<?xml version="1.0" encoding="UTF-8"?>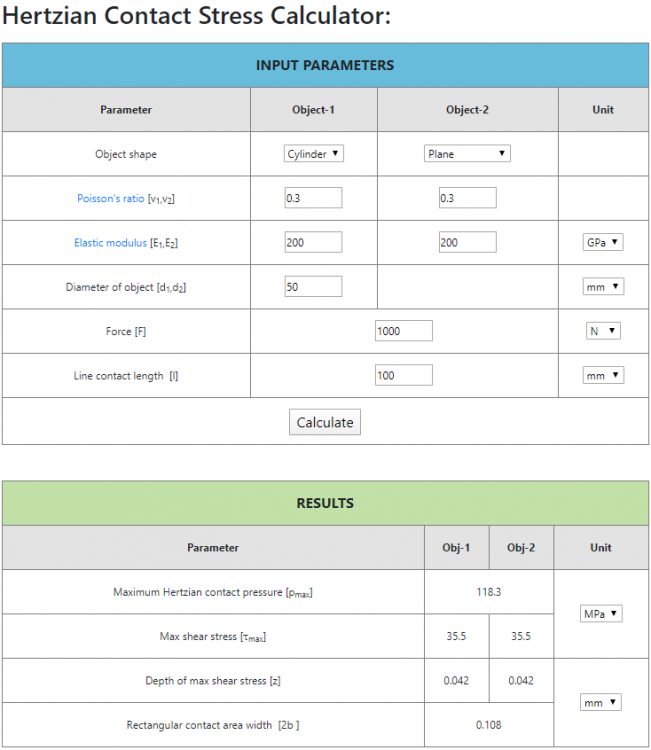
<?xml version="1.0" encoding="UTF-8"?>
Do you have any idea on why is this the case? Searching on the internet I realized that many studies in which Hertzian theory predictions are reproduced via FEA use a much finer mesh in the contact area: can this be the only reason for such a big difference in results?
Thank you in advance to anybody who will be willing to help me or to give me his point of view: any suggestions are welcome.
Best regards,
Manuele