マススケーリング（１）
陽解法では、これ以上Δtを大きく出来ない、という安定条件が存在し、これがCourantの安定条件と呼ばれる以下の式：
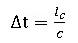ここにlcは要素の代表長さ、cは弾性波速度、
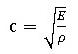、E:ヤング率、ρ：密度
で近似できる事は、時間積分の安定性について（１）、（２）で示した通りです。安定限界は、要素の安定限界は節点の質量と剛性でも与える事が可能で、この場合、
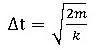、ここに、m：節点質量、k：節点剛性
となります。安定限界はモデル全体での最小の時間ステップΔtで決まり、モデル中に少しだけでも小さな時間ステップの部分があると、そのために計算時間が大きく伸びてしまいます。もし、その時間ステップを決めている節点に多少の質量を追加する事が出来れば、その分安定限界を大きく出来ますので、計算時間の節約になります。これがマススケーリングと呼ばれるものです。
マススケーリングはEngineファイル(0001.rad)の中で
/DT/NODA/CST
ΔTsca ΔTmin
というカードで指定できます。ここに、ΔTscaは安定限界に対する時間ステップのスケールファクターで、デフォルトは0.9です。これは安定限界の0.9の時間ステップで計算する事を示しています。係数を小さくするほど計算自体は余裕代が増えますので計算は安定しやすくなりますが、計算時間は増えます。一般に非線形性の高い問題を扱う場合には0.67位まで小さくした方が安全です。ΔTminがマススケーリングで目標とする最小時間ステップです。大きくすれば計算時間は減りますが、その分、節点に追加される質量も増えることになり、解くべき問題を変えてしまう事になります。どの程度質量が増加したかは、Engineの出力ファイル(0001.out)のMASS ERR.に出力されます。一般には2%( MASS ERR.が0.02)位までであれば、結果に対してそれ程影響を与えないと言われています。モデルにも依存しますが、この程度までの質量増加でも時間ステップを数倍大きくする事が可能になる事がしばしばです。ΔTminの大きさに関しては、Engineを少しだけ実行するなどして、MASS ERR.の値を確認し、決めます。
モデルの要素や節点の最小時間ステップは、Starterの出力ファイル(0000.out)にも出力されますので、これを確認してメッシュの修正が可能であれば予め修正して時間ステップが大きくなるようにすべき事は当然ですが、複雑なモデルですべての修正は困難な事が多いため、こうしたマススケーリングが実際には多く併用されます。