Product = GTAM/GSAM
Genesis® for ANSYS® Mechanical (GSAM/GTAM) adds the power and versatility of Genesis® structural optimization capability to the ANSYS environment. In this article, we would like to show how to perform topology optimization for thermal-mechanical coupled systems. Topology optimization is to find the optimal distribution of material in a given package space. Total strain energy (compliance) is typically used as objective to create a stiff structure. However, when there are thermal conditions presented, optimizing total strain energy does not give the correct results. In addition, when there are both thermal conditions and other static loads (force, pressure, etc.) in the same loadcase, if you would like to use strain energy as objective, you need to split this single loadcase into two loadcases: one loadcase with thermal conditions only, and one loadcase with other static loads. Now let’s explain why total strain energy cannot be used for optimization of thermal-mechanical coupled systems, the strain energy options in GSAM/GTAM, and why we need to split the loadcase when there are both thermal conditions and other static loads (force, pressure, etc.) in the same loadcase.
- Strain Energy Options in in GSAM/GTAM
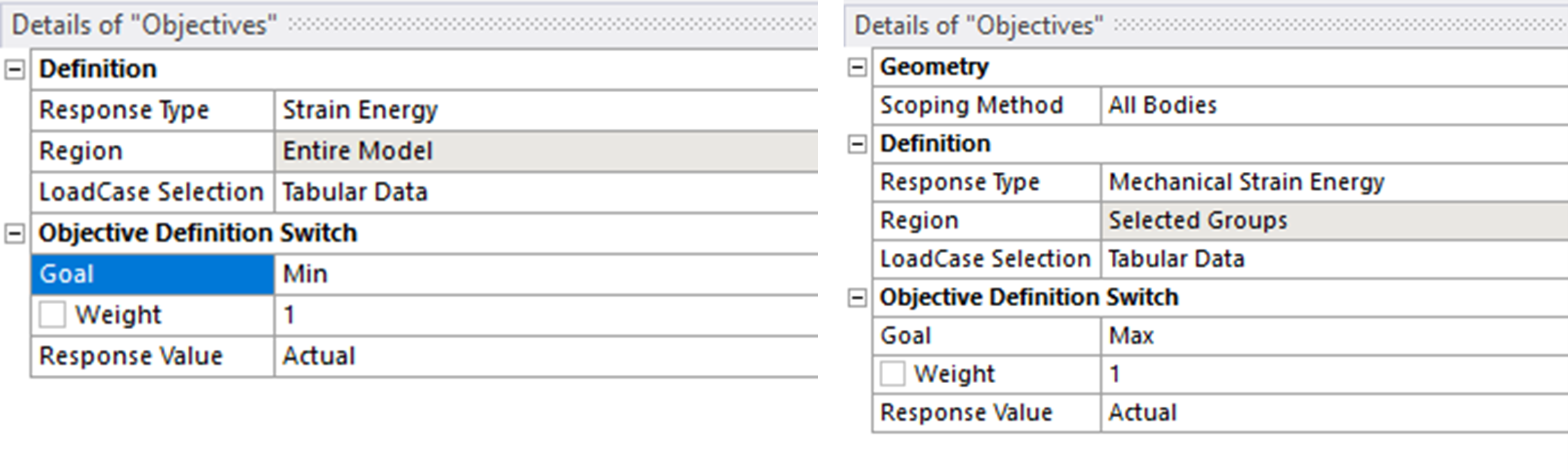
There are two options for strain energy in GSAM/GTAM: 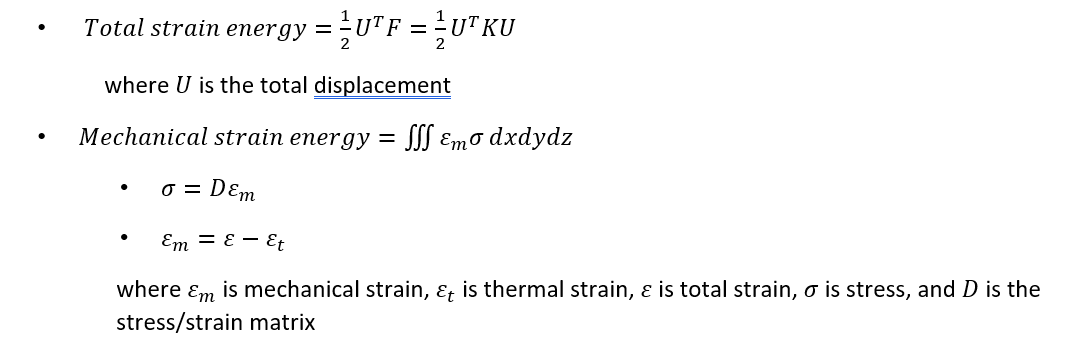
The main difference is that total strain energy ignores the thermal effect, while mechanical strain energy includes the thermal corrections. If there are no thermal loads, then total strain energy should be equal to mechanical strain energy for the whole structure.
- Why total strain energy cannot be used for optimization of thermal-mechanical coupled systems
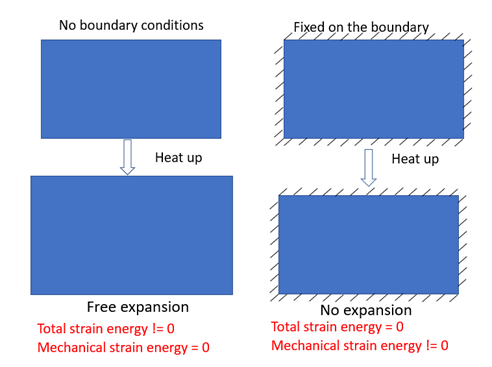
Let’s demonstrate this using the following simple 2D plate example. In the first case, there is no boundary condition applied. When the plate is heated up, it is free to expand. The total strain energy is not zero in this case since deformation is not zero, while the mechanical strain energy is zero. In the second case, there is fixed boundary conditions on the edge. When the plate is heated up, therefore there is no expansion. The total strain energy is zero in this case, while the mechanical strain energy is not zero. It is clear that total strain energy ignores thermal effect. If you choose to minimize total strain energy in the second case, it won’t give you a connected structure.
- Why We Need to Split Thermal Loads and Other Static Loads into Separate Loadcases
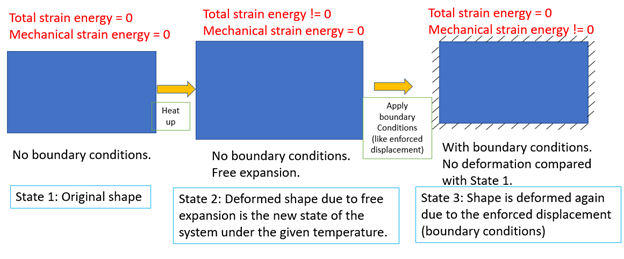
Thermal conditions are similar to enforced displacements. Let’s illustrate the temperature loading stages with the 2D plate as shown in the image below. The baseline structure (shape) for optimization for systems under temperature loading is the “state 2”, not the “state 1”. The temperature loadings create a condition similar to applying enforced displacements onto the structure. Therefore, when use strain energy as objective, just as we cannot mix enforced displacements with other static loads, we cannot mix temperatures with other static loads either. Meanwhile, we need to use ‘Maximize’ for the objective (mechanical strain energy), because we want to maximize the sustainable loading (temperature) on the structure that produces the same displacement (enforced displacement).
The following table shows what objective to use for each loadcase:
| | Loadcase with thermal conditions only | Loadcase with other static loads only |
| Objective | Mechanical Strain Energy | Strain Energy (Total) |
| Min or Max for Objective? | Max | Min |
- Examples
4.1 Topology optimization for static analysis with thermal conditions only
The analyses are defined as below. In static analysis, the four corners are fixed. 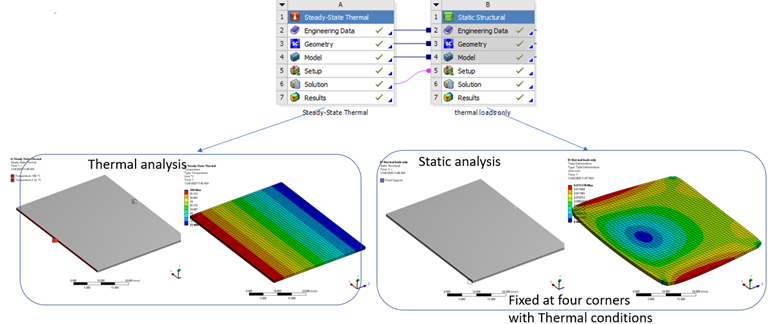
The topology result is as below. By maximizing mechanical strain energy, it gives a well-connected structure from loads to boundary conditions. While if minimize total strain energy, the structure is disconnected from boundary conditions. 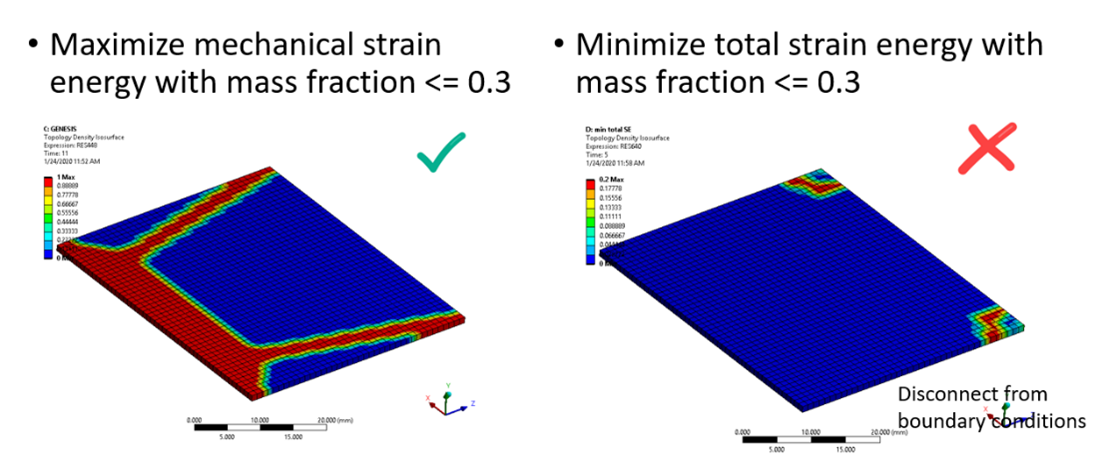
4.2 Topology optimization with thermal conditions and force
The analyses are defined as below.
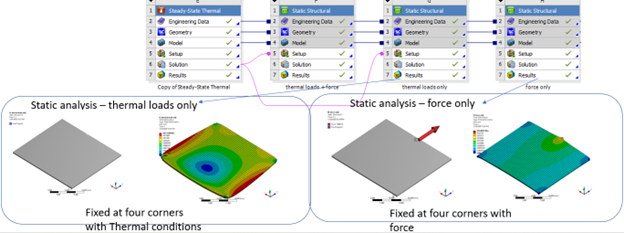
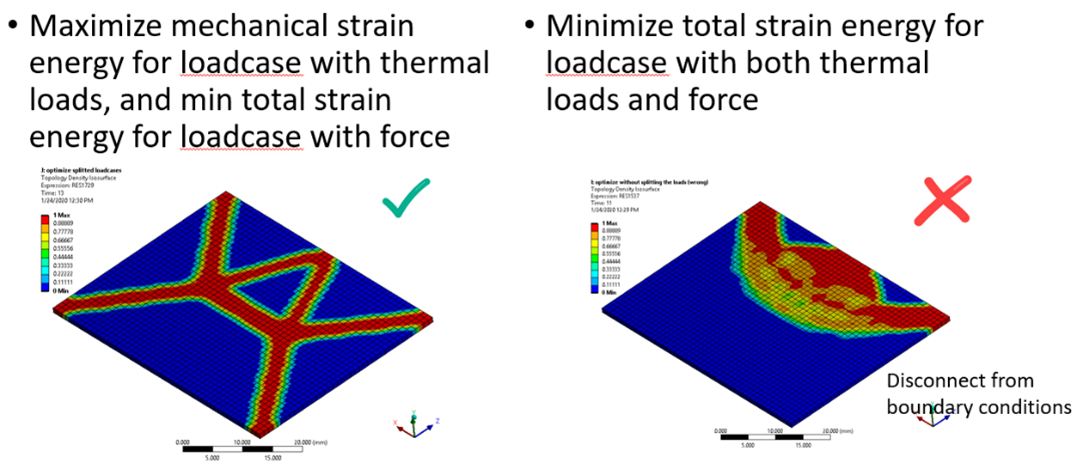
In static analysis, the four corners are fixed, and there is a force applied at the middle of one edge. We split the static loadcase into two static loadcases. In one loadcase, there is only temperature loading, and in second loadcase, there is only force applied. The topology result is as below. Similarly, by maximizing mechanical strain energy, it gives a well-connected structure from loads to boundary conditions. While if minimize total strain energy, the structure is disconnected from boundary conditions.
- Summary
As a summary, mechanical strain energy needs to be used in case there is temperature loading since it accounts for the thermal effect. If there are both temperature loading and forces in the same loadcase, if you plan to use strain energy, then the loadcase needs to be split into two loadcases: one with thermal conditions only, and one with forces only. If you have other requirement (ex. Stress) which needs to be applied for the condition when both thermal conditions and forces present, then you can apply this requirement for the original unsplit loadcase.
Note: In the GSAM/GTAM example manual there is one example that is similar to the example here. The name is ATP021, in which we optimize for both a thermal loadcase and a static loadcase. This example also talks about mechanical strain energy. If you have any questions or need any more information, please leave a comment below.