romAI検証コーナー（その11）Physical Informedアプローチ
Altair Employeeシンプルなモデルを使用して、romAIの機能をチェックしていきます。第11回はPhysical Informedアプローチについて確認します。
Physical Informedアプローチとは
PINNs (Physical Informed Neural Networks)のように、機械学習に対し積極的に物理方程式を取り入れるアプローチです。流体現象において、初期条件、境界条件、ナビエストークス方程式を学習データとして、Neural Networkにより流れを予測する例が有名です。
ほか、SINDy（Sparse Identification of Nonlinear Dynamics、非線形力学のスパース同定）があります。微分方程式の形を多項式や三角関数など仮定した上でそれらの係数を同定することで、非線形力学を再現する微分方程式を求める手法です。
romAIは微分方程式を予測しますが、PINNsやSINDyのように式の形（ナビエストークス方程式、多項式、三角関数など）は必要ありません。すべてNeural Networkが学習する点で大きく異なります。
ただし、romAIは非常に汎用性の高い手法です。微分方程式の形があらかじめ分かっている場合は、その情報を学習データとして追加することで、係数のみをすばやく同定することが可能です。まさにSINDyのような使い方にも対応できます。
問題設定
第10回で使用したvan der Pol方程式を考えます。
第10回では、van der Pol方程式の形を知らないという条件で、romAIがNeural Networksにより予測できるかを検証しました。
今回はvan der Pol方程式に非線形項x^2 vが存在することを知っているが係数のみが分からない状況を仮定します。romAIにx^2 vという物理情報を教えることで、より簡単にvan der Pol方程式が再現できることを示します。
学習データの準備
van der Pol方程式の非線形項を右辺に移動すると、線形の1自由度ばねマスダンパーモデルにx^2 vに比例した外力が与えられているという式になりました。
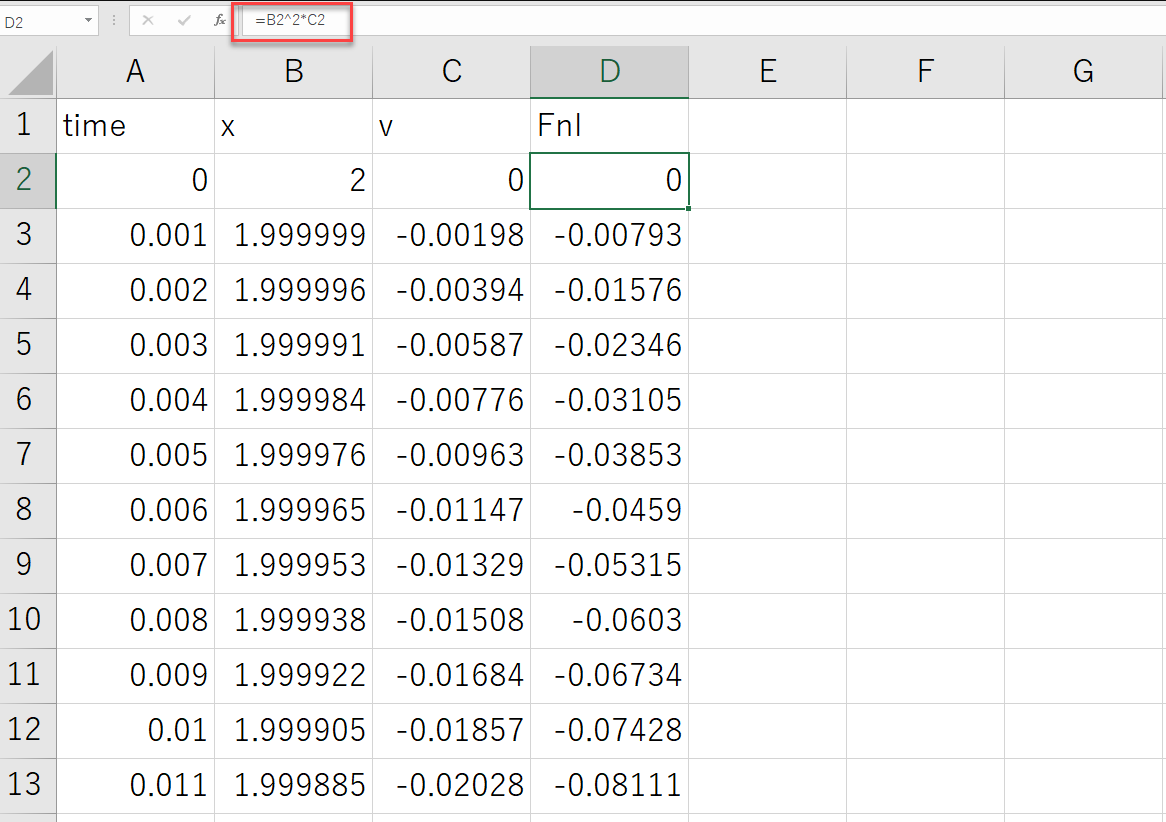
したがって学習データとして、x,vのほか、Fnl=x^2 vを追加します。
以下のような学習データが準備できました。今回は非線形性の強いmu=5のみとしています。
romAIの設定
romAIの設定を行います。出力、状態量ともに変位と速度とするほか、入力としてFnl=x^2 vを設定します。
Inputs: Fnl
Outputs: x, v
States: x, v
Physical constraintsを使用して、状態量同士の微分関係（変位xの微分が速度vであるという関係）を定義しています。
x^2 vが既知と仮定すると、すべて線形方程式となりますので、Model Typeはlinarとします。
Epochsは20としました。
romAIブロックの使い方
romAIブロックには入力ポートがありFnl=x^2 vを入力する必要があります。
下記のように作成した入力を接続してください。
計算結果
非線形性の強いmu=5条件でもたった20回のepochで再現できました。
まとめ
romAIは非常に汎用性の高い手法です。微分方程式の形があらかじめ分かっている場合は、その情報を学習データとして追加することで、係数のみをすばやく同定することが可能です。
今回はx^2 vのみを追加しましたが、例えば、SINDyのように３次までの非線形性を考慮したい場合は2次の項（x^2, xv, v^2）と3次の項（x^3, x^2 v, x v^2, v^3）を学習データとして追加してトレーニングを実施してください。romAIは係数自体の出力はできませんが、内部的にはx^2 v以外の項の係数はゼロとなり、van der Pol方程式が再現できるはずです。
Comments
-
本ブログで使用したモデルとその解説動画は下記よりご利用いただけます。
パラメータを変えていろいろお試しください。
https://community.altair.com/community/?id=kb_article_view&sysparm_article=KB0121925
0 -
本ブログでは、学習データにFnl=x^2 vを追加するためにActivateのモデルを修正して再計算しましたが、学習データはcsvファイルですのでExcel上で簡単に非線形項を追加することもできます。
0