FLUX3D - torque separation method using frozen permeability

Dr. Mandy Bauch

Dear all,

 

I would like to implement a macro for the separate calculation of the different torque components (cogging torque, reluctance torque and interaction torque) in 3D simulation of motors using the Frozen Permeability Method. I already derived the Frozen Permeability method for the 3D case from the existing 2D macro. 
 

I found a suitable method in Baserrah, S. Theoretical and Experimental Investigations of a Permanent Magnet Excited Transverse Flux Machine with a Segmented Stator for In-Wheel Motor Applications. Dissertation, Universität Bremen, Bremen, 2014. (page 238).

<?xml version="1.0" encoding="UTF-8"?>

 

In the first step I would like to calculate the cogging torque using the stored magnetic energy (the Frozen Permeability Method is not yet required for this).

 

With the help of a sensor I can determine the stored magnetic energy. Since I take advantage of the symmetry and periodicity of the motor and simulate only a part of it, I have to multiply the result by a factor. The derivation according to the rotor angle roughly gives the course of the cogging torque, but with strong fluctuations compared to the calculation via 'TorqueElecMag(ROTOR)' (see image below).

 

 

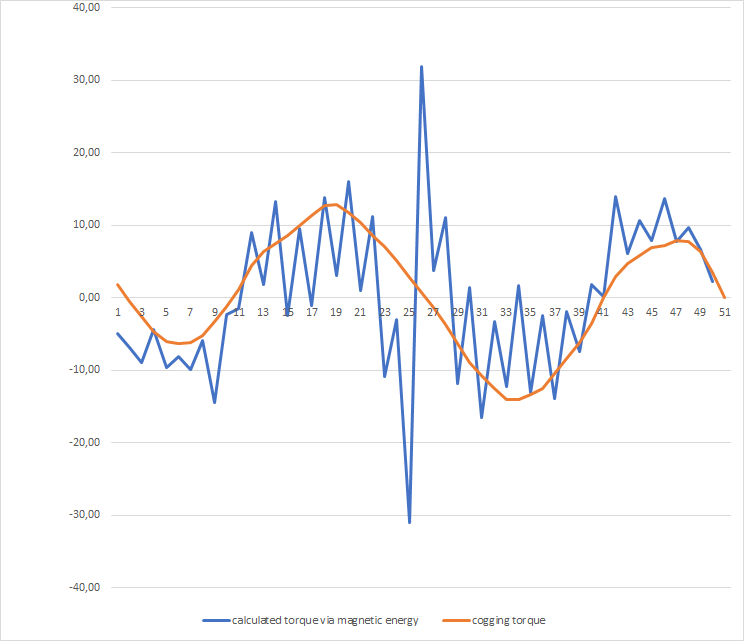
Does anyone have any idea what may be the cause of this deviation? I have concerns about using this procedure to calculate the reluctance torque, because large deviations are also to be expected here. Can anyone give me a hint on how to extract the reluctance torque from the simulation?

 

Many thanks in advance!

Mandy

Alejandro Rodríguez

Hello Mandy,

I understand your method to calculate cogging torque but I think it is rather difficult to applicate, since it implies to numerically calculate stored energy (not always an easy task) and them derivate it, which is also a tricky process from a numerical point of view.

In other words, to assure the accuracy of your results you will need a really dense mesh (especially in the areas where a high quantity of magnetic energy is expected to be stored)  and a small time step to be sure that your derivatives have enough precision. These two factor may lead the simulation time to skyrocket. Actually, seeing your results it seems that you need both, a denser mesh and smaller time step.

I am not an expert about torque components separation, but I can suggest you to check this paper, it may help you in your research.

[2014 Chen] X. Chen, J. Wang et al., “Reluctance torque evaluation for interior permanent magnet machines using frozen permeability”, 7^th IET International Conference on Power Electronics, Machines and Drives, PEMD 2014. (https://ieeexplore.ieee.org/document/6836779 )

Hope this helps.

Best regards,

Dr. Mandy Bauch

Dear Alejandro,

 

thank you very much for your reply and the paper's recommendation. It seems to be exactly what I need. 

 

According to my understanding it is especially important to have a fine mesh in the area of the air gap. Here I generally choose a 4-layer hybrid mesh, whereby I assign the volumes in the two central layers to the mesh generator 'mapped' and use an automatic mesh for the outer layers in the air gap. I also assign the mesh generator 'Mapped' to all stator and rotor surfaces facing to the air gap. Additionally, I limit the edge length of the mesh cells in the air gap by assigning a mesh line with minimum distance between the nodes to the corresponding edges. The number of mesh cells with poor quality is below 0.1%. I have only been working with FEM simulations for a few months, but I would say that the mesh is very good. Do you have any other tips for improving the mesh?

 

Nevertheless, I will have a closer look into the paper you suggested. At first sight only the Frozen Permeability method is required, which I have already implemented in 3D. 

 

Best regards,

Mandy