Deformation gradient F and Stretch tensor U in USER material routines
Dear all,
I have a question about the Deformation gradient F and Stretch tensor U in USER material routines. Do F and U already exist in Radioss routines? Because when I write a linear isotropic elastic material subroutine, I don't need to use deformation gradient F. But when I develop hyperelastic materials using USER material routines, I need to use deformation gradient F. Do I only need to declare F like this in engine subroutine, and then I can use them to calculate stress tensor directly because they already exist and are calculated automatically in Radioss?
DOUBLE PRECISION .FPSXX(NEL),FPSYY(NEL),FPSZZ(NEL), .FPSXY(NEL),FPSYX(NEL),FPSXZ(NEL), .FPSZX(NEL),FPSYZ(NEL),FPSZY(NEL)
Here is a slide from a tutorial of Radioss User Subroutines:<?xml version="1.0" encoding="UTF-8"?>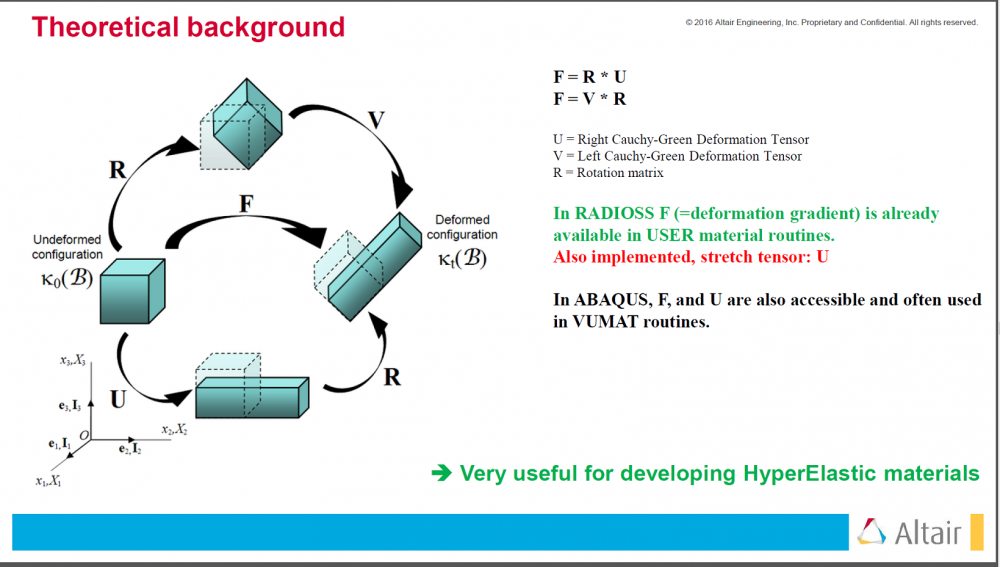
Besides, for 'Extended User Material Laws', in Chapter 3 of 'RADIOSS User's Code Interface', the data structure USERBUF doesn't contain FPSXX, FPSYY, FPSZZ etc. Which confuses me is how to use Deformation gradient F when write Radioss usermat subroutines? More precisely, if F already exists in Radioss routines, I only need to declare them and use them directly?
<?xml version="1.0" encoding="UTF-8"?>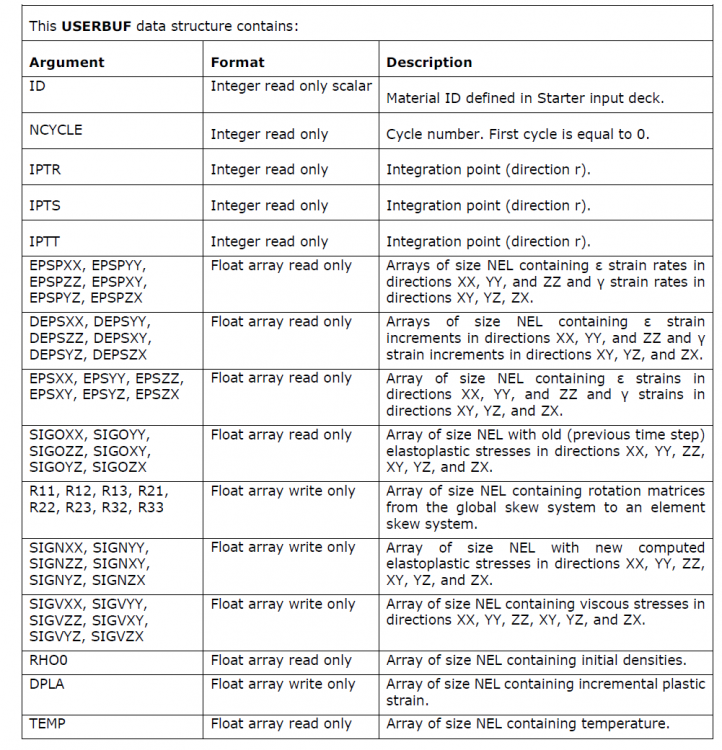
Could someone answer my question? Any help would be appreciated.
Best
Find more posts tagged with
Thank you Andy, your response is quite useful for me.
The deformation gradient variables are stored in the USERBUF data structure. However, they were not documented before but will be documented in the next version.
Another question is: I'm now using Radioss v14, is it necessary to update Radioss version? Or I only need to write and compile the subroutine according to the newer documentation?
Best
Hi,
I would recommend upgrading if possible. The latest version available is 2019.2. It might work to just use the new documentation with v14 but I am not really sure as I don't have a list of all the things that have changed for the user library since version 14.
Thanks,
Andy
Get it! Thank you Andy!
Best
Yes they both exist.
Yes you need to declare F because every variable must be declared as recommended by FORTRAN.
The deformation gradient variables are stored in the USERBUF data structure. However, they were not documented before but will be documented in the next version. I have attached newer documentation which includes the deformation gradient tensor stretch tensor and the rotation matrices from the global skew system to an element skew system.
Unable to find an attachment - read this blog