Tensor output in hwascii
Altair EmployeeHi there,
as showed in the picture I've got a problem plotting stress Tensors in inclined elements with Hyperview.
<?xml version="1.0" encoding="UTF-8"?>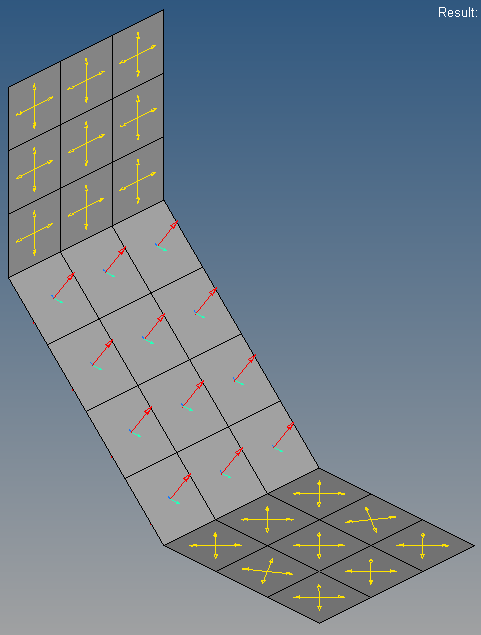
The idea is to show some calculated stresses after the postprocessing and it's realized with an hwascii-File as result file. But as shown in the middle, the Tensor isn't oriented like the element but shows an 3 component. In the end it should look like the tensor on the bottom/top.
Where do I have to look for information how to manipulate the output for an better result?
Thanks for your help!
Find more posts tagged with
Altair Employeeyes, it's just one HWASCII-file.
I'm not sure how to calculated the correct Tensor.
Where can I get the information about the six values of the (tensor-)matrix I have to pass to the HWASCII?
Are those the values of the diagonal plus the three upper entries of a symmetric or a triangular matrix?
Altair EmployeeHave a look at HWASCII help,
For example,
file:///C:/Program%20Files/Altair/13.0/help/hwdref/hwdref.htm?altair_ascii_reader_examples.htm
Altair EmployeeI've searched there but there isn't much information how the Tensor input must be calculated.
The visualized vectors of the tensor are the eigenvectors. The length of each vector is the corresponding eigenvalue. The three vectors must be orthogonal (so the matrix is symmetric).
Is that correct?
thanks for your answers so far!
Your screenshot is got from only one HWASCII file?
If yes, I think the problem is within your HWASCII. Check it please!