Density in material PLAS_JOHNS

Altair Forum User

Hello,

 

I am simulating a pull out test of a screw from an elastoplastic material ( MAT_LAW2, PLAS_JOHNS). The imposed displacement velocity that I apply on the screw is a lot higher than in reality. Before I used an elastoplastic material with a much higher density (probably like an excessive mass scaling) than the real one because it speeded up the simulation and the results did not change a lot. 

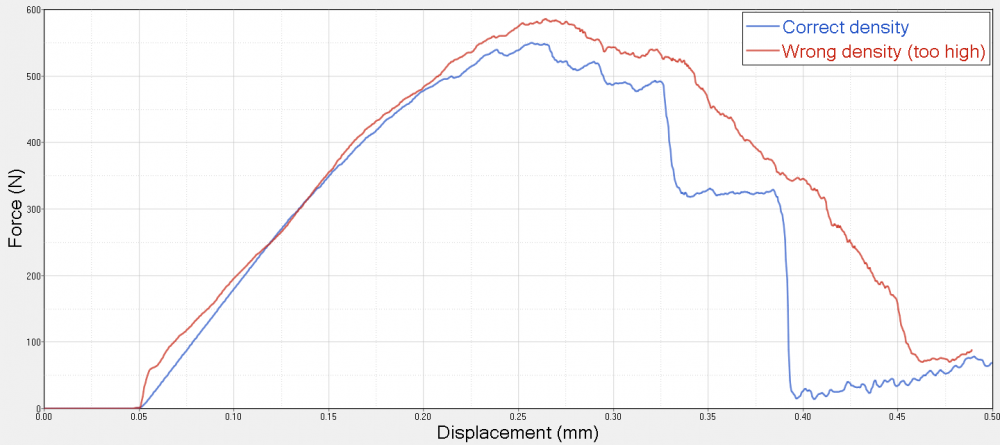
When I now perform the simulation with the correct density, I obtain curves which have sudden drops after the maximum force (see figure attached) is reached and from the .h3d file it seems that this is caused by a simultaneous deletion of many elements on one side of the screw.

I do not think that this latter behavior is correct and I wanted to know if someone has a suggestion on why this is happening. Can it be due to dynamic effects? What is the role of the density in the computations?

<?xml version="1.0" encoding="UTF-8"?>

Altair Forum User

Hi @Marie

 

Could you please share the files?

Nachiket Kadu_22143

Hi

This could be an issue of time step. The time step must be small enough to excite all frequencies in the finite element mesh. This requires such a short time step that the shock wave does not miss any node when traveling the mesh. Such a time step is given by relation:

δT ≤ Lc/c where c=Sqrt(E/ρ ).

ρ=density of material E= youngs modulus.

Nachiket Kadu_22143

What about the internal energy plot in both the cases?

Altair Forum User

Could be timestep as @Nachiket Kadu said, but such a sharp drop..?

 

any changes in the material data and/or model?

Andy_20955

Hi,

I doubt this is an issue with the time step.  Radioss calculates the highest timestep based on the desnity, modulus and mesh size as mentioned by Nachiket Kadu. 

 

The change in density/mass could cause the part to fail sooner.  It depends how much mass you were adding before and how close the part was to failing.  As already suggest check the kinetic energy in both models.  If it is a quasi static test then the kinetic energy should remain low in both models. 

 

The importance of mass in the simulation is the same as the importance of mass in the test.  In both the test and the simulation if the mass is different the physic and energy will be different which can cause a difference in the results.

Thanks,

Andy

Altair Forum User

Hi,

 

Thanks a lot for the fast replies.

I did not apply mass scaling so far, thus the time step was set by the solver. The only difference between the models is the density of the material, but this difference was very large. It should be a quasi-static model. 

<?xml version="1.0" encoding="UTF-8"?>

<?xml version="1.0" encoding="UTF-8"?>

Altair Forum User

Hi again,

 

I also noted that if I use the correct density but in addition I add the kinetic energy relaxation card (/KEREL), the FORCE-DISPLACEMENT curve becomes similar to the one obtained with the wrong density.

<?xml version="1.0" encoding="UTF-8"?>

<?xml version="1.0" encoding="UTF-8"?>

Altair Forum User

Hi

 

/KEREL sets all velocities to zero when KE reaches a maximum. 

 

If you are using mass scaling, it is not recommended to use /KEREL

Altair Forum User

Hi,

 

thanks for the reply. I did not use the kinematic relaxation together with mass scaling. But using /KEREL or applying a higher density to the elements leads to similar results.

Could this mean that because I impose a much higher imposed displacement velocity, it would be better to use one of these two options instead of just using the correct density? In other words, are the results shown in the above green and red force displacement curves probably more correct than the ones in the blue curve?