Contact modeling is a critical component of multibody dynamics simulations, especially in applications involving latch mechanisms, robotics, electric tools, and similar mechanical systems. Accurate and efficient contact handling significantly impacts the realism and stability of the simulation.
Overview
In multibody systems, contact occurs when two or more bodies interact through direct physical touch. This contact can generate forces, impulses, or constraints that alter the motion of the involved bodies. Accurately capturing these effects requires a robust mathematical and numerical framework.
Contact modeling begins with collision detection, where the solver first identifies body pairs that may come into contact (broad phase), and then accurately computes contact points, normals, and penetration depths using geometric queries (narrow phase).
Once contact is detected, a repulsive force is generated at the contact region to prevent interpenetration by pushing the bodies apart. In most general-purpose multibody solvers, the repulsive force acting normal to the contact surface is implemented using penalty-based contact methods. These methods apply a force normal to the contact surface that increases with penetration depth, typically modeled as a virtual spring-damper system to approximate the physical behavior of contact.
Challenge
Penalty-based methods are relatively simple and robust compared to alternative approaches such as constraint-based contact formulations. However, they can introduce numerical stiffness, allow small interpenetrations, and most critically require careful parameter tuning. While modern solvers are generally capable of handling the numerical stiffness, selecting appropriate parameters is often left to the engineer.
For example, in the widely used impact model of the form F=K*z^exp*C(z), which belongs to the penalty method family, the engineer must define several parameters: the contact stiffness K, the exponent exp governing the force-deformation relationship, and a damping coefficient C. In simple cases, such as a rigid ball impacting a flat rigid surface, these parameters can be estimated from Hertzian contact theory.
However, real-world applications often involve complex, arbitrary geometries that cannot be simplified into Hertzian forms. In such scenarios, engineers must manually tune the contact parameters to produce behavior that appears physically realistic. This process is often tedious, time-consuming, and uncertain, especially in the absence of physical test data to validate the simulation results.
Solution
Most finite element solvers also use penalty-based contact formulations and typically handle them quite effectively. While the structural engineer must still define contact coefficients, fine-tuning is generally less critical, as long as the penalty stiffness is sufficiently high, typically three orders of magnitude greater than the stiffness of adjacent elements (i.e., K_penalty≈ 10^3 * 𝐸 * ℎ, where E is Young’s modulus and h is a characteristic element size).
The reasoning behind this approach is straightforward: restitution is primarily governed by the elastic deformation of the contacting parts, not by the contact method itself. The contact can be conceptualized as two springs in series as shown below.
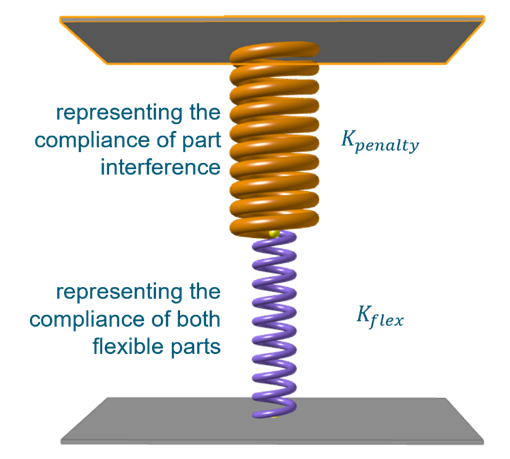
The lower spring represents the physical compliance of the flexible body, while the upper represents the penalty stiffness. The equivalent stiffness is
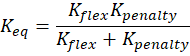
To ensure that the total repulsive force is dominated by the actual deformation of the structure (rather than artificial compliance introduced by the penalty term), the penalty stiffness must greatly exceed the structural stiffness, K_penalty » K_flex. Let's assume that K_penalty = 10^3 * K_flex, then we easily see that the equivalent stiffness is
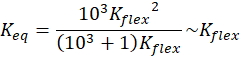
This same principle can be applied in multibody simulations by replacing rigid bodies expected to undergo contact with flexible body representations. Multibody tools like Altair MotionSolve are particularly effective at handling contact interactions involving flexible bodies, allowing for more accurate and physically meaningful simulation of contact dynamics.

Recommendation
We recommend that engineers follow several best practices when defining contact in multibody simulations:
- Permanent Contacts: When rigid bodies are permanently in contact, such as in hinges, sliders, or similar mechanisms, these connections should be modeled using joints defined by kinematic constraints. Altair MotionSolve offers a wide range of joint types, including revolute, spherical, and translational joints, as well as higher-pair constraints like point-to-curve and curve-to-curve joints. These are commonly used in applications such as cam-follower systems, where geometric motion relationships must be precisely enforced.
- Intermittent Contacts: In cases where bodies come into contact intermittently, contact modeling should be used. If the geometries are primitive shapes, such as spheres, cylinders, or boxes, the contact parameters can often be derived using Hertzian contact theory, which provides analytical expressions based on material and geometric properties.
- Arbitrary Geometries: When contact involves arbitrary or complex shapes, a more accurate approach is to model the rigid bodies as flexible bodies. This requires specifying appropriate material properties, including Young’s modulus, shear modulus, and Poisson’s ratio. The penalty stiffness in such cases can be effectively estimated as two to three orders of magnitude greater than the effective stiffness of the flexible body. This ensures that the repulsive force is governed by the body’s structural deformation rather than by artificial compliance.
Summary
The penalty-based approach relies on a soft contact assumption, requiring careful tuning of stiffness and damping coefficients. Improper parameter selection can lead to two common issues: excessive interpenetration if the stiffness is too low, or numerical instability if it is too high, sometimes resulting in unrealistic behavior such as bodies accelerating uncontrollably or moving at implausible speeds.
To reduce the burden of parameter tuning, rigid body contact can often be replaced with flexible body contact. This approach allows the deformation behavior of the structure to naturally govern the contact response, minimizing reliance on artificial stiffness values. In Altair MotionSolve, flexible body contact modeling has been extensively refined over the years to specifically address the challenges and limitations associated with rigid and flexible body contact.
Altair Inspire, which uses MotionSolve as its motion solver, takes this concept further by fully automating flexible body generation through just a few simple clicks. Engineers can quickly convert rigid parts to flexible bodies, enabling high-fidelity contact modeling with minimal setup. Try Inspire Motion and see the results in action.