The problem of static analysis of adhesive problem

mansin
mansin Altair Community Member
edited November 2020 in Community Q&A

Hi, everyone.

     I created a simple model of two rectangular plates connected by adhesives between them. In this model, all degrees of freedom are constrained at one side , the distributed force  is applied on the other side. The property of plates and adhesive are Steel and Epoxy Glue, respectively.

    (1) Why are there great differences between the stress distributions on two plates?  The stress level of the plate with constraints is much higher than the other plate, why?  (Is induced by the clamped constraints?) I think there are also problems with stress concentration and displacement.

    (2) Why is the stress level of adhesive so low? 

   Can anyone give me some advises?

   Thanks.

<?xml version="1.0" encoding="UTF-8"?>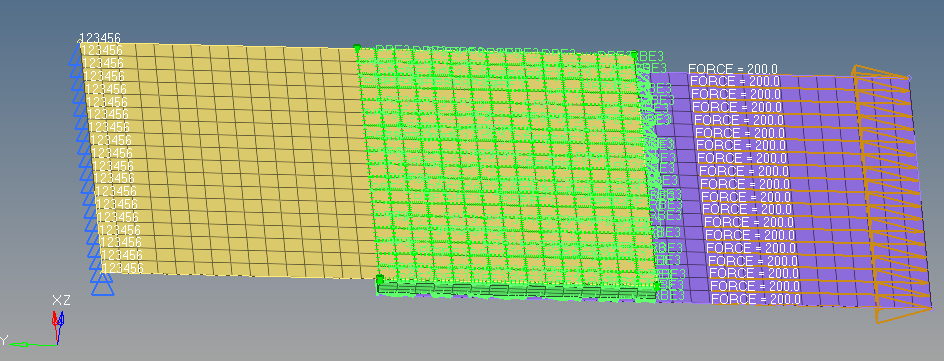Constraints and Loads.PNG

<?xml version="1.0" encoding="UTF-8"?>Stress.PNG

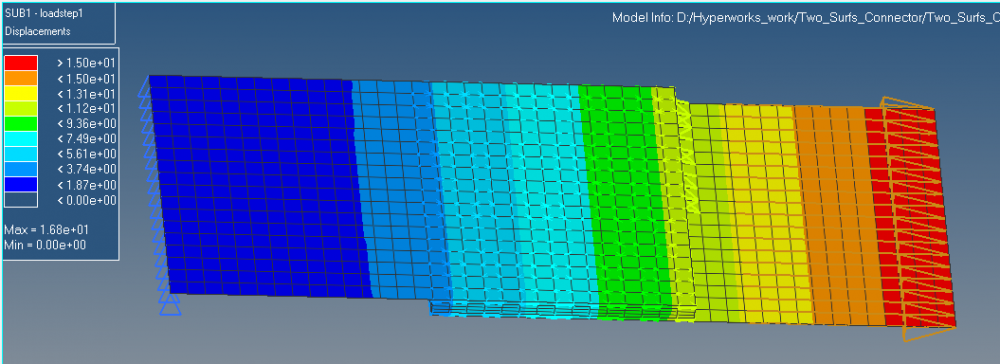
<?xml version="1.0" encoding="UTF-8"?>Displacement.PNG

Unable to find an attachment - read this blog

Tagged:

Answers

  • Altair Forum User
    Altair Forum User
    Altair Employee
    edited April 2018

    hi mansin,

     

    There is stress in the second plate also. You can check it by selecting only the second component like shown below.<?xml version="1.0" encoding="UTF-8"?>123.thumb.png.005f56d169b66686e1daf83d4cda646b.png

    Its only because of the scale factor, you are not able to see any stresses in the 2nd plate, while considering both the components.

     

     

    Thank you

     

  • mansin
    mansin Altair Community Member
    edited April 2018

    Hi, Premanand Suryavanshi,

    Thank you for your advise. I still have the question: Why are there great differences between the stress distributions on two plates? The stress level of the constrained plate is almost ten times higher than that of the other plate.

     

    Thanks.

  • Altair Forum User
    Altair Forum User
    Altair Employee
    edited May 2018

    Hi,

     

    The stress will always be more at the fixed end. Hence, it shows more stress in the top plate.

     

    Thank you

  • Altair Forum User
    Altair Forum User
    Altair Employee
    edited May 2018

    Hi,

    For a clamped model like this it will always tend to break from the fixed end as all the dof is arrested here. And that's why you're getting high stresses at fixed end.

     

  • Mario_21478
    Mario_21478 Altair Community Member
    edited May 2018

    Hello,

     

    It is quit simple. Due to the distance between the two plates, there is a bending moment at the clamped plate (plus axial load).

    In the free plate is only the axial stress. You can check it, it's about 11 MPA (3800N/3500mm*mm=11MPa) nearly constant (global Sigma Y).

     

    Some general hints to adhesive modelling:

     

    • Normally you can't use a static solver for thick film bonding, depending on the stiffness of the glue
    • Normally thick film glue has a Poisson ratio near by 0.5 and extremely nonlinear material behavior
    • As example, if you want to glue with Sikaflex, then you have large strains. This isn't included in static linear or quasi static nonlinear. You have to use geometric nonlinear, be sure the solver supports large strains
    • A nonlinear 'standard' elastic plastic material isn't sufficient to describe the material behavior
    • Your maximum displacement is about 15mm, it isn't 'small' in terms of linear static
    • Depending on type of bonding you have to take into account creep and relaxation
    • Depending on load conditions you have to take into account dependence on strain rate effects

     

    I'm not a expert on this, but be sure it is a quit difficult topic.

     

    Best Regards,

    Mario

     

Categories