Dear all,
I'm working on a project as the attached image shown: We want to increase the natural frequency of the blue plate by design reinforcing components attach to the plate.
Therefore we set up a design space (green block). The objective is max mode 1 frequency of the whole model, and constraint is max 0.5 volume fraction of the design space.
However as the second image shown:
1. Mostly only the element on the edge of the design space are left, and it's easy to understand they WON'T help to increase the plate natural frequency at all;
2. The mid elements circled in black are 'floating', meaning they are not attached to the plate at all.
Could anyone help to figure out what I may do wrong in the setup?
Thank you,
Peter
<?xml version="1.0" encoding="UTF-8"?>
<?xml version="1.0" encoding="UTF-8"?>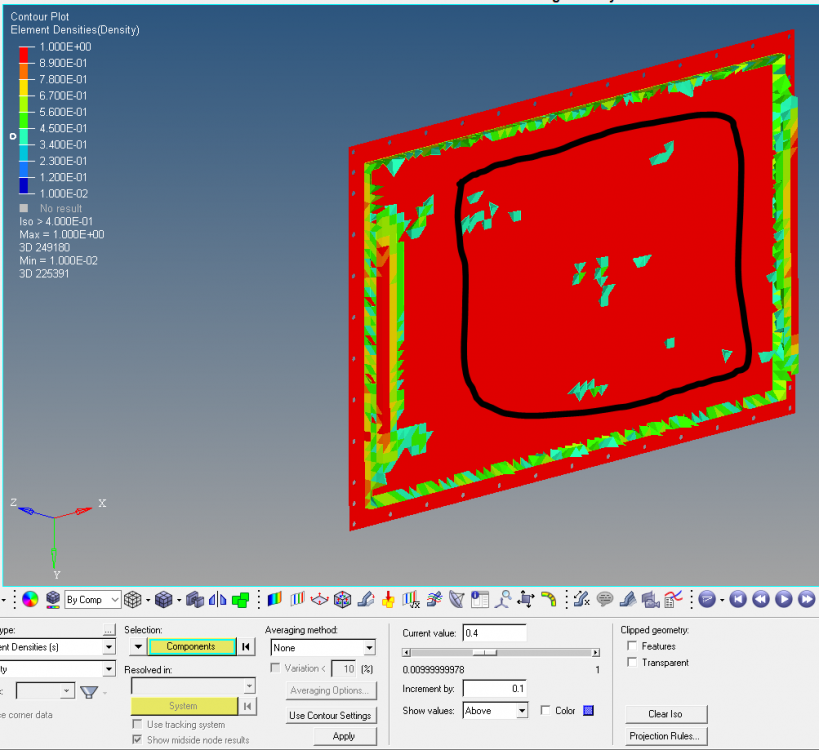
Unable to find an attachment - read this blog