We are often biased by our prior knowledge of physics, and that might not be a bad thing.
Let's try a thought experiment.
Imagine that you have trained a machine learning model to predict how an airplane bracket will bend. Let's say that the bracket is constrained at the four bolt holes and has a vertical load applied to the center.
Here are predictions from two hypothetical models, models A and B. Which one would you say is better?
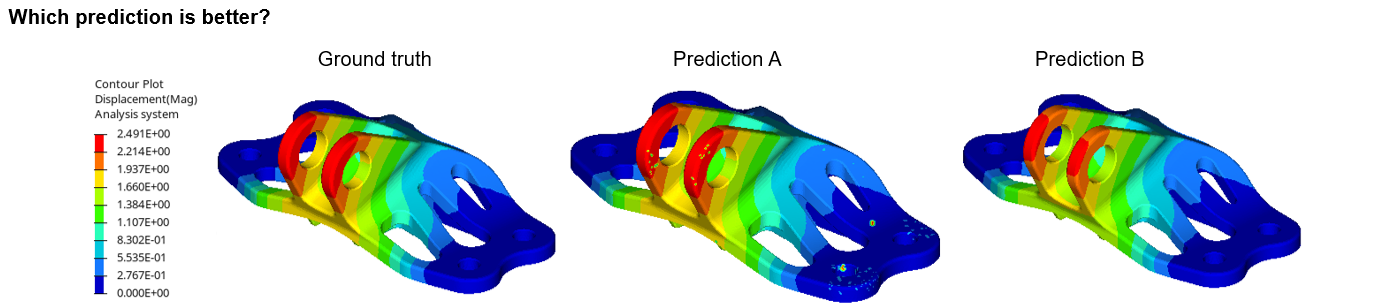
My immediate reaction is that something is wrong with prediction A. The displacement field has hotspots in seemingly random locations. There are even nonzero displacements where I know for a fact the model is constrained. This can't possibly be, so something seems off.
Now let's quantify the prediction accuracy using common error metrics (note that there are many others):
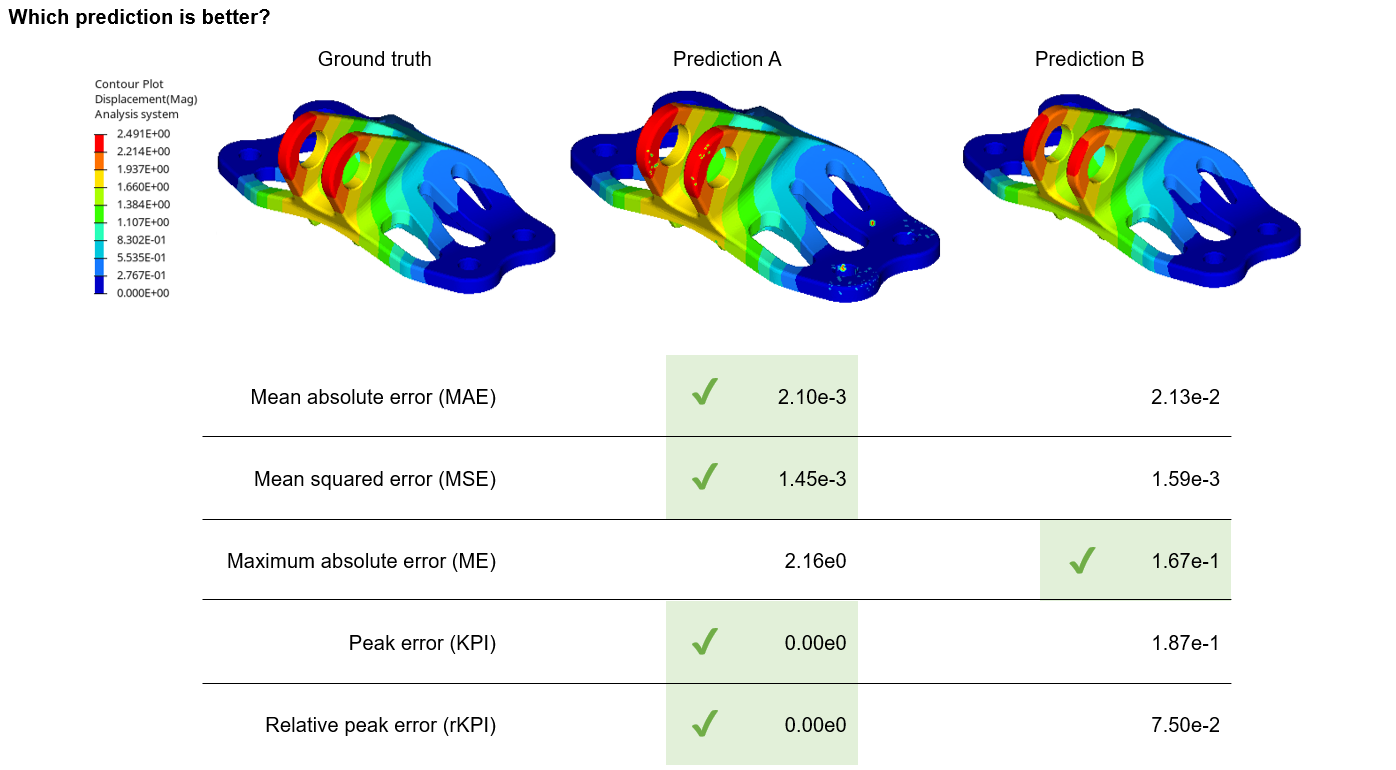
Uncanny hotspots aside, prediction A is superior to prediction B in every error metric but maximum absolute error. Again, which prediction is better? Did these metrics change your answer?
The truth is that I'm not entirely sure which is better.
On one hand, one could confidently argue that prediction A is more useful. The maximum displacement is likely a key performance indicator (KPI), and is predicted quite accurately. The general trend of the bending response is also correctly predicted despite the anomalies. Prediction A would seem to supply the necessary information to make a design decision.
On the other hand, something about prediction A makes me uncomfortable. I think it's because it violates my prior knowledge about physics and materials. Prediction B might have worse error metrics but at least it is a "feasible" outcome, right?
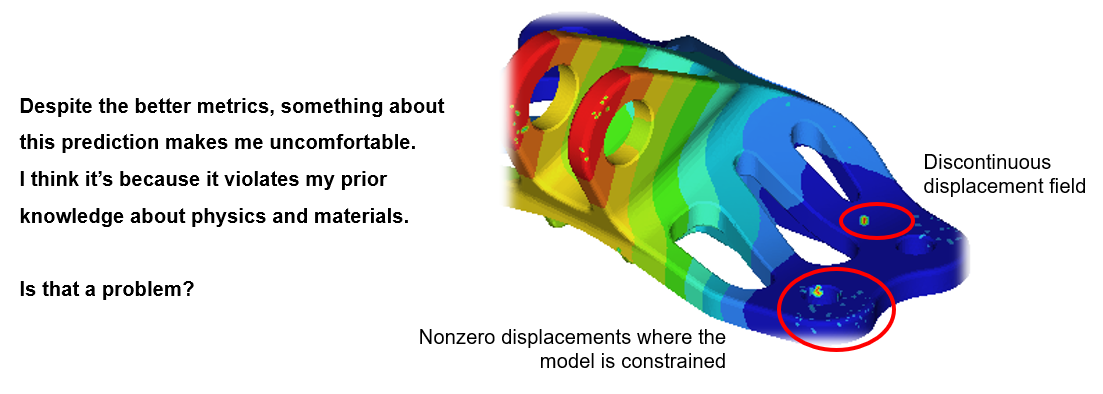
In statistics, this consideration of prior knowledge in the face of new evidence is known as Bayesian thinking, and it can protect us from being mislead by data. It can also improve our models. When models are designed to exploit prior knowledge about a particular problem, these exploitations are known as inductive biases. For example, convolutional neural networks (CNNs) exploit the translational invariance of images, and physics-informed neural networks (PINNs) exploit the known governing equations. A central challenge in designing machine learning algorithms is to exploit the inductive biases of the problem at hand.
In fact, one reason why the finite element method has become so popular is that it comes with guarantees that the solution is optimal for the selected basis. The solution might not necessarily be accurate, but these guarantees do rule out a large portion of the solution space which cannot possibly be correct. A solver would never produce something like prediction A. I would argue that this is a form of inductive bias as well.
A central challenge in designing machine learning algorithms is to exploit the inductive biases of the problem at hand.
So which prediction is better? I'm inclined to say that prediction A is more useful to an engineer (if we were designing video games, it might be a different story!). At the same time, I also think it's important to listen to your gut when you feel like something is off. Can you investigate why model A is producing spurious hotspots? Why is it that the solution space for your model contains solutions that are so obviously nonphysical? These questions are the first steps in improving the algorithmic design.
I'm curious to hear your thoughts. Do you have a lower tolerance for non-physical errors, or is all error the same? Can you think of an error metric that would penalize these nonphysical artifacts?