Improving Mesh quality

Simon Neuner

Dear Experts,

 

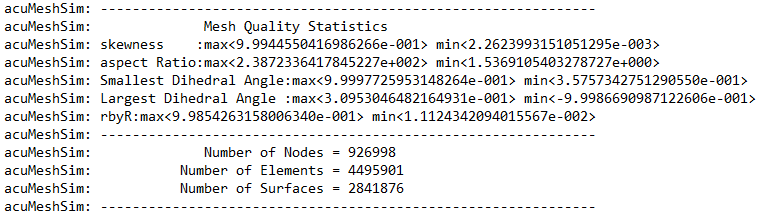
I have a solar panel consisting of five layers, where two dimensions are much larger than the third dimension (by a factor of about 200-300:1). I have already meshed the component very fine in the plane and get the following statistics from AcuMeshSim:

 

 

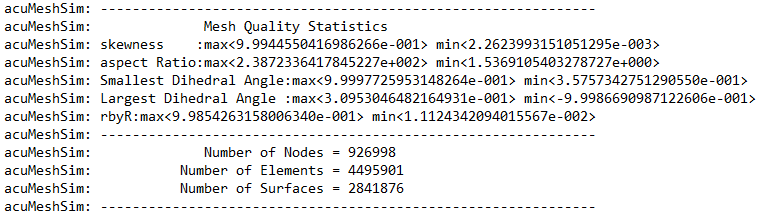
As a setting I tried the following options to minimize the skewness of the elements:

<?xml version="1.0" encoding="UTF-8"?>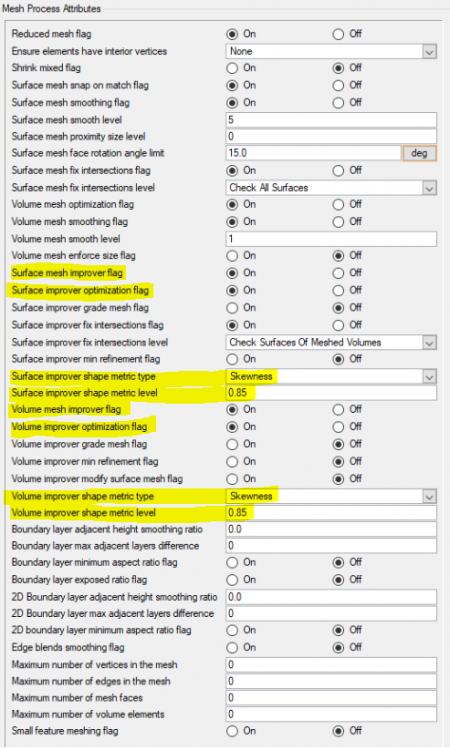

Additionally I tried the option Surface Mesh Proximity Size Level with values of 1-3, but my PC does not seem to have the necessary computing capability for this.

 

I have already read that AcuSolve is very generous in terms of element quality and focuses more on the distribution of the nodes.
If no big temperature gradients are expected, one could estimate if the existing element quality is sufficient or not?
If not, which options could I try?

 

Thanks in advance!

<?xml version="1.0" encoding="UTF-8"?>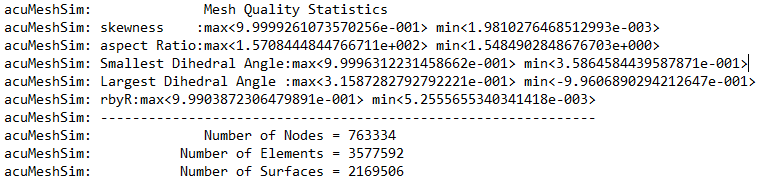

<?xml version="1.0" encoding="UTF-8"?>

acupro

This sounds like a perfect candidate for multi-layered thermal shells.  These are basically zero-thickness volume elements where the number and properties of layers are specified in the element definition.

Simon Neuner

Altair Forum User said:

This sounds like a perfect candidate for multi-layered thermal shells.  These are basically zero-thickness volume elements where the number and properties of layers are specified in the element definition.

 

Dear /profile/5282-acupro/?do=hovercard' data-mentionid='5282' href='<___base_url___>/profile/5282-acupro/' rel=''>@acupro, thank you for your adcive!

 

What about the boundary conditions at the interface between two materials - if surfaces of two thermal shells are adjacent, can I define the contact conditions separately?

 

Additionally, I read that only one-dimensional heat conduction over the thickness of the thermal shell can be computed, but I would like to calculate three-dimensional conduction. Is there a possible option for that problem?

acupro

With thermal shells there is no physical surface between layers.  The layers are just defined to compute the overall thermal resistance for the entire set.  Conduction is solved in all directions - but again it would be using the overall thermal resistance - not a layer-by-layer conduction model.