CMA Mode Tracking Far Field

christian1

Hello,

 

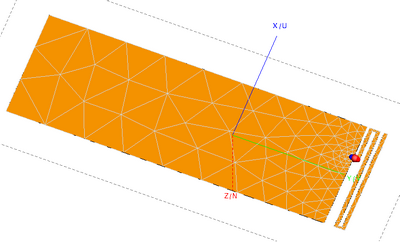
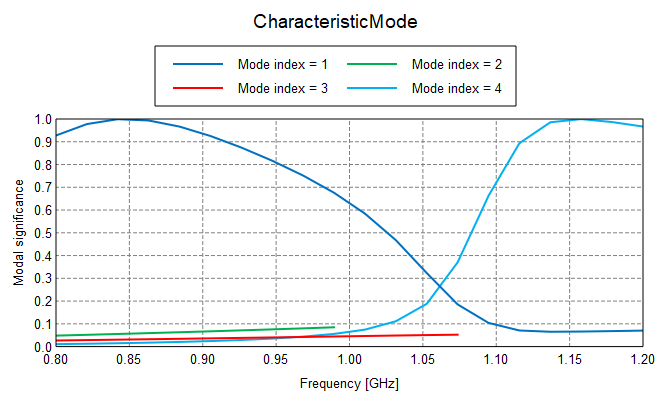
I am trying to understand the results of the CMA of a meandered monopole on a ground plane. The modal significance plot shows two dominant modes (mode 1 and 4). The curve looks smooth and consistent so I expect no mode tracking error here. However, when I look at the far field patterns of the modes and cycle through the frequencies (see below) I noticed that the patterns change very drastically. Mode 1 seems to be the lambda/2 dipole mode at 850 MHz (doughnut pattern) but it changes very quickly above 1.1 GHz. Mode 4 starts as a double-doughnut (similar to 2xlambda dipole) but changes into the single doughnut shape at 1.2 GHz.

The total radiation pattern obtained through 'Standard configuration' changes only very slightly.

So my question is how to interpret the quickly changing far field patterns. I know that FEKO is tracking the modes according to current densitiy correlation. But shouldn't there be some consistency of the far field patterns, too? Is there a tracking error? Or is this the expected characteristic? I am just starting out with CMA.

Thanks,

Christian

 

 

 

<?xml version="1.0" encoding="UTF-8"?>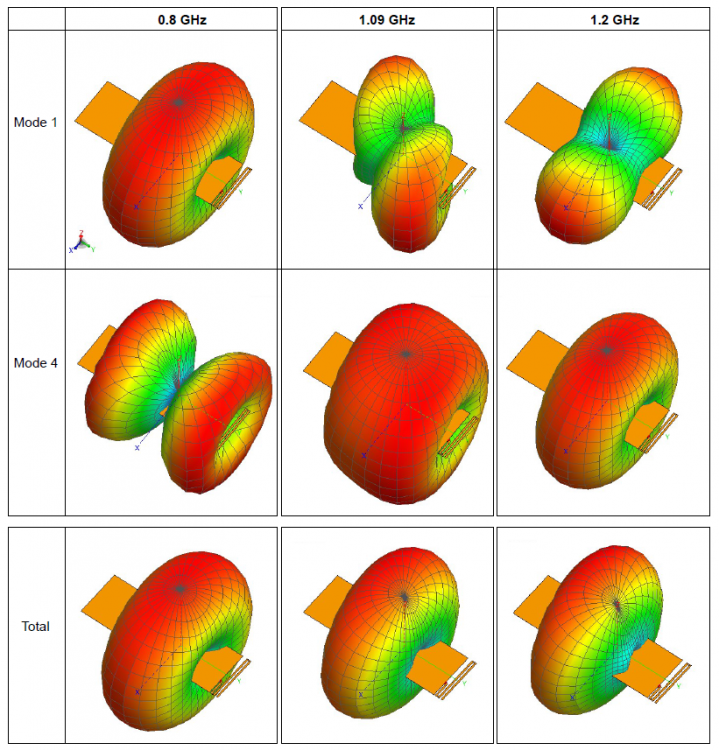

 

Unable to find an attachment - read this blog

Wilco Strydom

Hi Christian,

Interesting problem to look at for a beginner in CMA.

 

The first thing I did with your model was to run a simulation with 20 samples in [1.05, 1.07] to see if there was any interaction between the modes.

Since there was none, I wont now go into details of cross avoidance and whether or not that is desirable.

 

Let me answer some of your questions directly:

... shouldn't there be some consistency of the far field patterns, too?

Yes, but similarly to current density correlations, only between immediately adjacent frequencies.

 

Is there a tracking error? Or is this the expected characteristic?

There is no tracking error.

While this might sound strange, Characteristic Modes can and do change their characteristics over frequency, but they do so gradually. Looking at far field patterns, or at instantaneous currents* (particularly insightful of how the mode changes) you can see how each step in frequency is only a gradual change.

 

In your case it so happens that Mode 1 at lower frequencies has the same characteristics of Mode 4 at higher frequencies.

Looking at Modal weighting coefficients (always valuable when antennas are involved) shows that at any one point it is the dipole mode that is most excited, hence the total field value observations.

 

*If you switch on arrows for instantaneous currents, note that the current is prone to 180 degree phase jumps from one frequency to the next, so the arrows might flip on you. This is because the current is on both sides of the eigen equation: X*J = lambda*R*J