Understanding the TH file

Hi,

I am trying to interpret my results for a sloshing simulation using interface loads. Unfortunately, I cannot attach all my results due to the size of the model, however I am running it in two parts: One using KEREL and one using AMS. The KEREL is used only to settle the SPH, before the sloshing begins in the AMS portion of the simulation. To my understanding, sloshing simulations should show a single peak for interface forces at the point where slosh is at a peak, however my T01 file has various up and down peaks, while the T02 file shows a linear increase in interace force until the end of the simulation. I am not sure which interface force graph to trust (if either, because it does not seem consistent with reality either way). Furthermore, based on observations in the model stresses, it seems the interface load is on the order of 8e5 only in very specific spots, even though the elements are highly refined. Would appreciate any suggestion.

Thanks in advance.

<?xml version="1.0" encoding="UTF-8"?>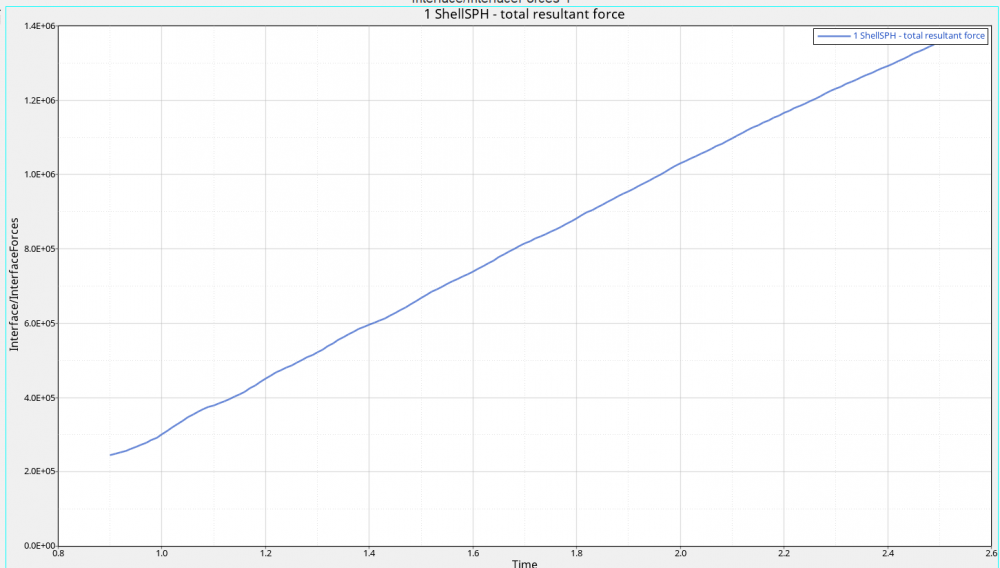

Unable to find an attachment - read this blog

Find more posts tagged with

English

Radioss

Accepted answers

All comments

Simon Križnik

Hi,

it would be useful to have the animation (my workstation is too weak for this model)- use the HVtrans tool to reduce the file size to upload limits (only stress, contact forces and displacements; reduce frames if necessary).

Verify the AMS run against a CST (or without mass scaling) run with a reasonable energy error (ERROR < +2%) and acceptable added mass (MAS.ER < 0.02) along its simulation time.

Crashphys

Hi,

Thank you for your time. This is my mass error time-history plot with only CST:

image.png.c9ce8279d32ea0ea9c7db4ad969d56c9.png

The energy plot with AMS is:

image.png.21fb2ae5269e54c2bf9f4bc3de298849.png

/KEREL is applied in the first 0.9 seconds without AMS, which is why you see those peaks at first. Energy error is -0.2% total by end of simulation and stays near zero for most of it.

I plotted the F-t diagram logarithmically on the Y-axis and is does seem to show somewhat of a constant load, but I do not know if this actually is accurate.

I am including my H3D file from 0.9 seconds to 1.75 seconds here. The relevant simulation time is 0.9 seconds to 2.5 seconds. I will include the second part from 1.75 seconds to 2.5 seconds in the next post.

Unable to find an attachment - read this blog

Crashphys

Was not able to upload across two posts unfortunately. I tried to compress with a higher error but it completely scrambles the mesh. Here are my TH files.

Unable to find an attachment - read this blog

Simon Križnik

The animation file is not available for some reason. Can you share it through Google Drive?

Compare the interface forces between AMS and CST runs on the same plot.

It is strange that T01 and T02 plots not matching in trend nor the magnitude.

Crashphys

Hi Simon,

Thank you for your continued help despite technical issues. Please see the link below for the whole model:

https://drive.google.com/file/d/1wK9cGuk0CiQ_WDQM9eyLtPDtatouQig1/view?usp=sharing

I went ahead and ran it without any mass scaling (took forever) and the results are agreeable with AMS, so I do not think it is possible the AMS is the issue. See image below, light pink and green is the AMS run, others are from no mass scaling at all. I also plotted on a logarithmic scale. I do not know if this is valid, but if so, then it may indicate that the force interface is behaving as expexted...

<?xml version="1.0" encoding="UTF-8"?>

Thanks in advance.

Simon Križnik

Since the AMS run matches other runs without time scaling, the conjugate gradient is below 30 and energy error stays low throughout we can conclude the observed behavior is not an artifact of AMS and the run can be considered verified.

Because I haven't researched sloshing I am not able to comment on the validity (matching physical behavior), but I can provide my explanation of the simulation results.

There is not a single peak, because the lateral acceleration is ramped up, is held for .8 s then ramped down. The cargo 'sticks' to the wall as long as there is lateral loading- instead of bouncing right off. A single peak would be expected if the impulse was a lot shorter (without hold period) or there was an initial velocity imposed on the model. However, I think the acceleration pulse used is consistent with the railcar cornering.
The lateral load is ramped up over a period of .3s which excites the bending eigenmode in the sidewall. In the graph below, the X displacement in the region of the highest amplitude of vibration is plotted. The period of vibration of the sidewall coincides with the period of vibration of the contact force; the hypothesis is as the sidewall vibrates against the cargo the contact forces exhibit pulsating forces in phase with sidewall vibration.

Therefore the T01 seems consistent with the expected behavior (given the boundary conditions). But I have no idea why T02 does not overlap the T01 trend.

<?xml version="1.0" encoding="UTF-8"?>

Crashphys

Hi Simon,

This is a very interesting and clever observation. I could not have come to this conclusion alone for sure. I suppose this could very well happen in a realistic situation, however the vibration amplitude is crazy high +/- 1.5 cm or so...

The thing is, if the cargo sticks to the wall, my intuition tells me it should be absorbing the vibration energy, so it shouldn't be possible that this fluctuation is so high.

Do you know of any documentation dealing with how the total interface force is calculated? Is it some sort of sum of all the loads? I was thinking it is possible that the load may also be fluctuating because as the particles are lifted by lateral acceleration they lose some contact with the wall (for ex the particles near the bottom of the car), but then they make contact with the rest of the SPH further driving them in?

While the acceleration profile makes sense, I just can't see how total interface force can fluctuate as much as 200,000 N which is approximately 10% the weight of the cargo.

Either way, thank you for the observation.

PS, Not able to message you privately, so I am posting here: I do not know if you are comfortable with it or if you are interested, however I am currently writing up my thesis and you have helped me greatly with my work over its course. If you are interested, I would like to add you to my acknowledgements. I can use your name tag here if you like, or I can temporarily put up contact information if you want to associate your name/work with the acknowledgement.

Thanks again

Simon Križnik

The amplitude of vibration is high because there is no damping in the second step. The damping effect is more pronounced at frequencies near the resonance peaks. The worst-case scenario is when the excitation frequency (ramp-up period) is near the resonant frequency and there is no damping. When you are unsure about the damping, perform a sensitivity analysis by varying structural damping in the realistic range and observe how much the responses of interest are affected. The proper amount of damping should also reduce interface force fluctuation.

Unfortunately, I do not have the documentation on how the total interface force is calculated, but it is probably the sum of all contact forces. Your explanation is plausible, but it does not account for the period of vibration.

p.s. I would appreciate being acknowledged in your thesis. Actually, your challenging queries also sparked my interest in the subject therefore I would like to have a look at your thesis.