Altair RISE

A program to recognize and reward our most engaged community members

Nominate Yourself Now!

Composite thickness increasing stress??

Hi,

I am modelling sandwich panels applied to a wall with loading in various cases. In sandwich theory, the stress should decrease with core thickness. However when the core is thick here, the minimum principal stress is much higher than when the core is thin.

I am aware there is a high load specifically at this point in specific so stress is high, however stress should still decrease with increased thickness. I am wondering if anyone has an explanation to help me understand?

Thin Composite:

<?xml version="1.0" encoding="UTF-8"?>

Thick Composite:

<?xml version="1.0" encoding="UTF-8"?>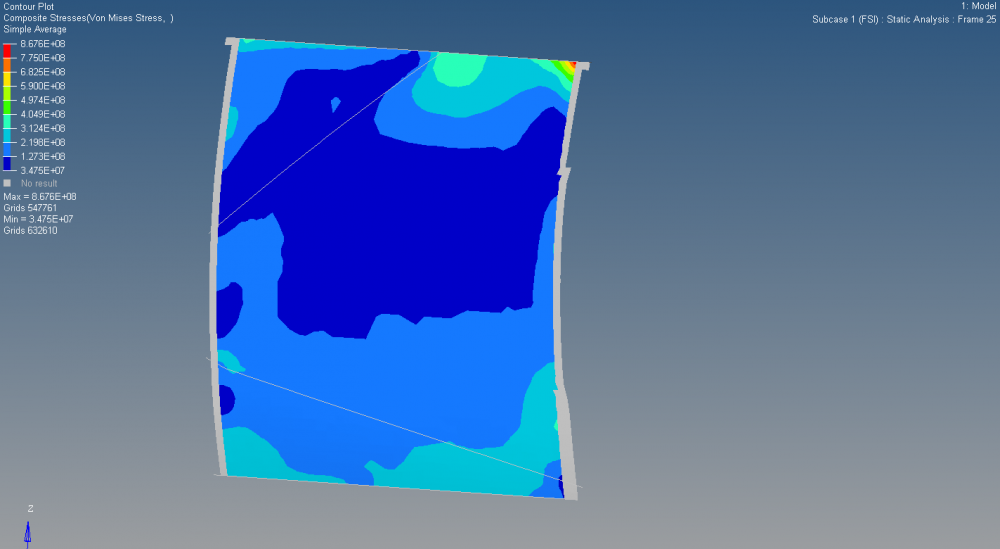

Unable to find an attachment - read this blog

Find more posts tagged with

English

OptiStruct

Accepted answers

All comments

Simon Križnik

Hi,

These counterintuitive results can be explained if the displacements are imposed: the thicker structure is stiffer and develops more stress under the same imposed displacements.

For similar reasons when optimizing for stiffness:
-imposed loads= minimize compliance
-imposed displacements= maximize compliance

Crashphys

Hi Simon,

Thanks again for the help. In this case, loads are applied and not displacements. That's what makes it all the more confusing...

Worth mentioning also: For all load cases, compliance appears to increase with increased core thickness.

Simon Križnik

While there are forces and moments in the FSI_LOADS load collector, there are also imposed displacements on the model boundary as a result of breakout modeling. Running without any loads results in non-zero displacements.

Unable to find an attachment - read this blog

Crashphys

Hi Simon,

I guess this is not so much a software problem but a theoretical one but:

Considering there are both loads and displacements applied here, if I wanted to optimize this is there a way to address this if I wanted to run OS optimization with stress constraints?

Simon Križnik

I haven't done breakout model optimization yet so take this with a grain of salt:

One way coupling is a limitation of breakout modeling: the boundary conditions transferred from the global model may not be valid in a local model, if the local model's stiffness is changed significantly (in a way that alters global behavior).

Check how the global response changes at upper when compared to lower bound stiffness (thickness). Afterward, perform optimization with a narrower stiffness range for which boundary conditions are still valid.

Also try including a more extended transition region.

You may find the following article useful:

https://www.digitalengineering247.com/article/global-local-modeling-fea/

Quick Links

All Categories
Recent Discussions
Activity
Unanswered
日本語 (Japanese)
한국어(Korean)
Groups