What method behind different Topology Optimizations?
Altair EmployeeHi,
I'm doing a topology optimization with Optistruct 13.
It's about a wheel carrier for a formular student car with 8 static load cases.
I've set up 2 different optimizations:
1. with the objective of min volfrac
2. with given mass (from 1. optimization) and min wcomp
Both with same modell and element size 1.5, mindim 4, maxdim off, Stress constraint of 110 and a max displacement for 8 nodes.
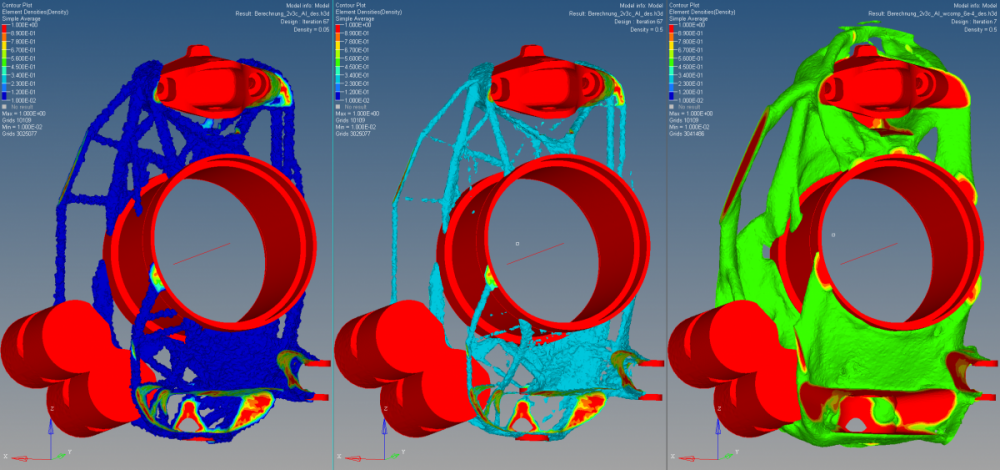
[1] For the 1. optimization a get a good looking result, but i have to set the density very low (0.05-0.1, left picture). Even with this value the reanalysis gets higher stress than the constraining. With lower values (0.5) there are unconnected elements (middle picture).
[2] For the 2. optimization the solver isn't able to calculate a result with the given mass of opt. [1]. With higher values it's getting results. There I have good results with density of 0.5, but it's to heavy (right picture).
I try to understand the differnt methode behind this 2 optimizations. Specially how it's setting up the density.
So my questions are:
- What are the method behind this 2 optimizations? [2] behave like it's described in the SIMP Method but in [1] it seems like there is no penality (according to SIMP)
- What's the different in the algorythem of this both optimizations?
- Why I have to set down the density so much for [1]
I've read a lot in the HW help, journals and books, but I'm not able to explain it, so thanks a lot for every answer.
<?xml version="1.0" encoding="UTF-8"?>
Answers
-
Hi,
How are you apply the stress constraint?
Can you apply from Topology panel itself (on DTPL card)?
From OptiStruct FAQs,
•
The definition of stress constraints is limited to a single von Mises permissible stress. The phenomenon of singular topology is pronounced when different materials with different permissible stresses exist in a structure. Singular topology refers to the problem associated with the conditional nature of stress constraints, i.e. the stress constraint of an element disappears when the element vanishes. This creates another problem in that a huge number of reduced problems exist with solutions that cannot usually be found by a gradient-based optimizer in the full design space.
•
Stress constraints for a partial domain of the structure are not allowed because they often create an ill-posed optimization problem since elimination of the partial domain would remove all stress constraints. Consequently, the stress constraint applies to the entire model when active, including both design and non-design regions, and stress constraint settings must be identical for all DSIZE and DTPL cards.
•
The capability has built-in intelligence to filter out artificial stress concentrations around point loads and point boundary conditions. Stress concentrations due to boundary geometry are also filtered to some extent as they can be improved more effectively with local shape optimization.
•
Due to the large number of elements with active stress constraints, no element stress report is given in the table of retained constraints in the .out file. The iterative history of the stress state of the model can be viewed in HyperView or HyperMesh.
•
Stress constraints do not apply to 1-D elements.
•
Stress constraints may not be used when enforced displacements are present in the model.
0 -
It's done directly in the Topology Panel.
The FAQ doesn't help.
Topology opt. is runing for tetra4 Elements, von Mises < 110 MPa, design+nondesign same material.
0 -
Since Stress constraint is a global response, it will try to reduce to the stress for both design and non design case.
In your set up 1 both objective and constraints are satisfied by reducing the stress on overall structure (material falling under this value is removed) and minimizing the volume at the same time. As you reduce the iso value this further removes the material and thus you will end up with more stress during re-analysis. Start with 0.3 value and there on...
But in your second setup you are trying to increase the stiffness by constraining the mass. Which may not give you good result in a single GO.
Maybe change the optimization set like Min Mass with displacement constraints or Min Compliance with a Volume Fraction constraint.
0 -
1.: I've see the is a mistake in the picturce. The middle one is with density 0.3.
Lowering the ISO value will show elements with lower density which results in more elements.
So for 0.3 there are free Elements and the result isn't productive.
Lower ISOs, like 0.1 is more or less productive, but stresses are to high.
Min Mass does the same like min volfrac.
Also min compliance with volfrac constraint does the same like given mass.
For me and my dissertation the point how it's done, what's the methode/procedure, the algorithm that are the interesting points.
Both Opts are done by using the density method / SIMP, right?
With Default OPTMETH in opti control what algorithm is used for this both cases? Is it the method of feasible directions (MFD)?
0 -
Hi,
We can't share the algorithm or any background information used by solver.
Sorry about that.
0