Hello,
I am working on an non-linear-quasi static model with pretensioned bolts and friction contacts.
I set up the model with first order elements first, this model was converging fast and results were ok.
in order to get the correct tensions i changed the elements to second order.
After this i recreated the contacts and pretension to make sure everything is correctly linked to the second order elements.
If i run this model it is taking days and doing a few iterations until it starts all over again and again.
I use surface to surface contacts and a value of friction of 0,14.
I am not sure why this is happening because everything is the same as in the first order elements.
Could you please help? I uploaded the out. file and did a few screenshots.
Thanks a lot!
<?xml version="1.0" encoding="UTF-8"?>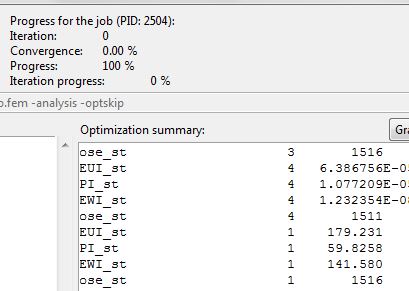 <?xml version="1.0" encoding="UTF-8"?>
<?xml version="1.0" encoding="UTF-8"?>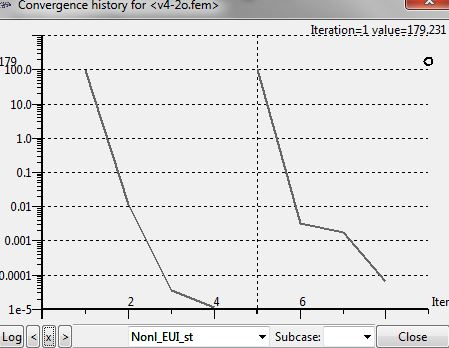
Unable to find an attachment - read this blog