Linear buckling analysis with linearly variable axial loading

Greetings,

 

I would like to calculate the critical buckling load Fkrit of a linear buckling analysis with the following linearly varying axial distributed load.

The starting load is Fo= 0,1 N which increased ends fixed in a wall after a range of 1000 Elements at F1=100 N.

 

 

<?xml version="1.0" encoding="UTF-8"?>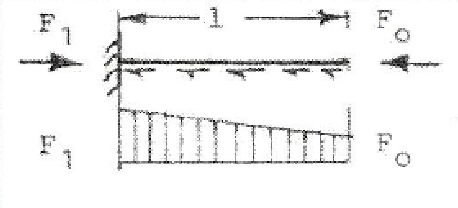

 

 

The geometric profile is a thin-walled cross-section with a length of 1000mm.

 

Hypermesh says the result of the lowest eigenvalue takes lambda_cr = 7.288 e-03

 

The critical buckling load P_Cr is defined as:

 

P_Cr = lambda_cr * P_ref

 

For a static case corresponds the force magnitude of one Force the P_ref value. (As shown in the tutorial linear buckling analysis)

 

I have two questions:

 

1. What would be the best way to implement the linearly variable axial load as equation? I mean distribute the force circumference or use rigids?

 

2. How can i determine the value of the P_ref for a linearly varying axial distributed load?

 

The analytical solution for P_Cr is something about 185 N.

 

 

Thanks in advance