Feko solver settings offer several options to choose different simulation approaches and sometimes it can be tricky to pick the best option for a simulation problem.
In this article we discuss use cases where curvilinear higher order basis functions have advantages.
The default option in Feko for MoM simulation are the traditional linear Rao-Wilton-Glisson (RWG) basis functions [1]. As alternative in 2013 hierarchical higher-order basis functions (HOBFs) up to order 3.5 were introduced [2]. They can be selected in general ribbon of the solver options:

What is the concept behind HOBFs?
The traditional way to improve simulation accuracy with RWG basis function is mesh refinement. This so-called h-adaptive approach is now being supplemented with a p-adaptive scheme, that improves the quality of the solution by selectively increasing the polynomial order of the elements. By choosing the default Auto option Feko will use the appropriate element order and mesh size to achieve sufficient accuracy.
Therefore, elements can be defined as a larger size for HOBF than for RWG basis functions. The CADFEKO mesher will take this automatically into account. For CEM modeling of general structures that may possess arbitrary curvature, it is essential to have both higher order geometrical flexibility and higher order current/field-approximation flexibility in the same method. This is ensured in Feko with curvilinear elements using second order triangle elements with 6 vertex points. Details about theory of HOBF for different simulation methods and for geometric modeling are described in [3].
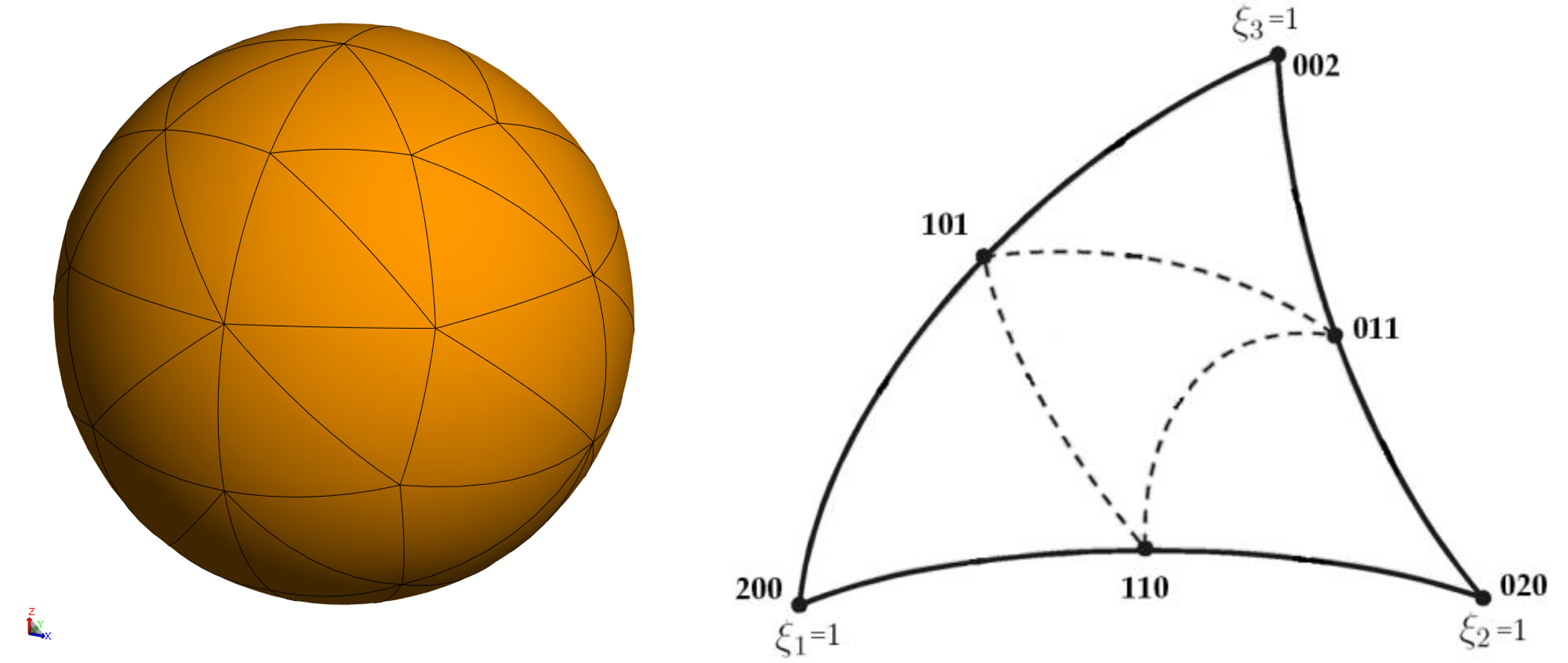
What are the main advantages when using curvilinear HOBF elements for MoM?
- Highly curved surfaces can be modelled with less elements with reduced geometrical approximation errors
- For electrically large models the number of MoM unknowns will be reduced with HOBFs. This allows the frequency range for MoM models to be extended upwards. Instead of switching from MoM to MLFMM as usual, MoM-HOBF is an alternative worth considering. Especially for problems with multiple right-hand sides – like RCS – this can speed up runtime, because the LU-decomposition of the MoM-HOBF matrix can be reused.
Let us first examine the geometric approximation: The picture shows typical use cases for segments and surface elements.

The helix curvature will be much better approximated with 1D curvilinear elements without changing the element number. And in the surface case the advantage of curvilinear elements is even bigger: With 184 planar triangles the sphere has clearly recognizable edges, where the tangent plane is discontinuous. In the curvilinear case a much smoother approximation can be realized with 60 curvilinear triangle elements.
The area of the meshed sphere depends on the discretization too. For the coarse mesh the area is just 96.6% of the original sphere geometry. This results in a lower and a slightly angle-depending Radar Cross Section (RCS). We used a PEC sphere with radius 1m and computed the monostatic RCS at 100 MHz.
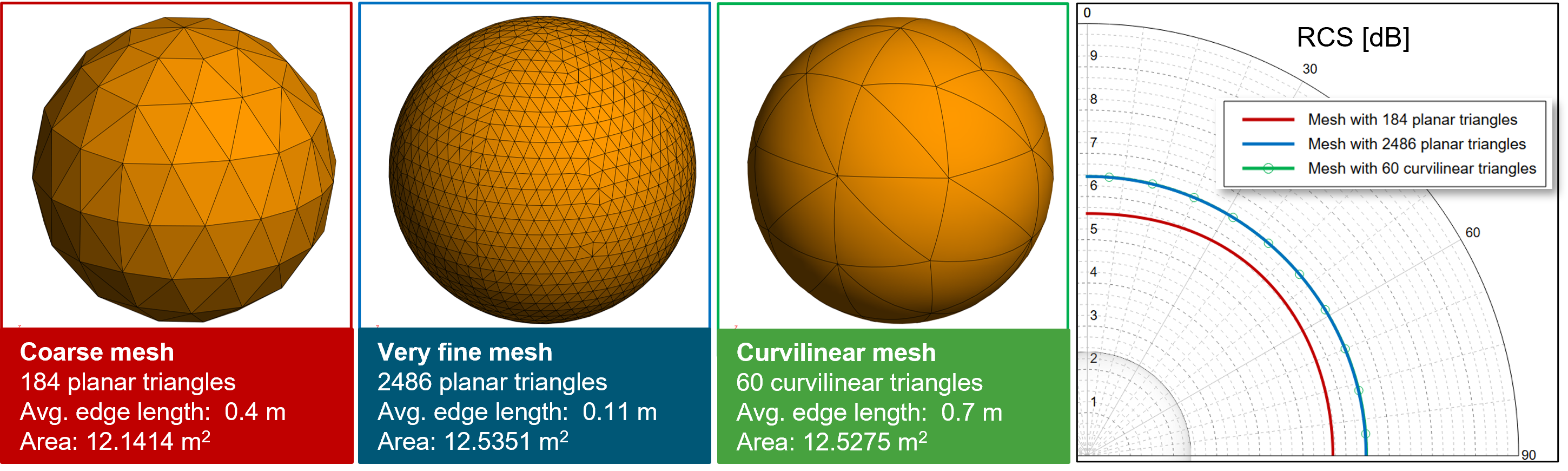
The coarse model underestimates the RCS by 0.7 dB. With fine mesh using planar triangles and with curvilinear mesh using HOBF the results are more accurate. Comparing performance indicators for both accurate results show speed improvement by factor 2.5 and memory reduction by factor 75 with the HOBF.
Geometrical flexibility of curved elements can be fully exploited only if they can be made electrically large, which implies the use of higher order basis functions within the elements as well. In order to make the modeling of realistic structures optimal, it is often convenient to have elements of different orders and sizes combined in the same model. In the Feko solver settings this will be realized by choosing the Auto (default) option. Alternatively, a fixed degree could be defined and the Feko mesher will consider this setting for the element size of the curvilinear elements: Higher element order allows larger element size.
The typical frequency range to solve a model with classical MoM and RWG basis function can be extended by switching to HOBF. Especially for problems with multiple right-hand sides – like RCS – the MoM-HOBF can even outperform MLFMM. We demo this behavior with a benchmark example [5] of a dielectric truncated cone at 9 GHz. With RWG basis functions the cone is meshed for MoM or MLFMM with 35554 planar triangle elements. With HOBF the same model could be meshed with only 338 curvilinear elements. Runtime and memory requirements are better with MoM-HOBF compared to MoM-RWG and MLFMM as shown in the table.
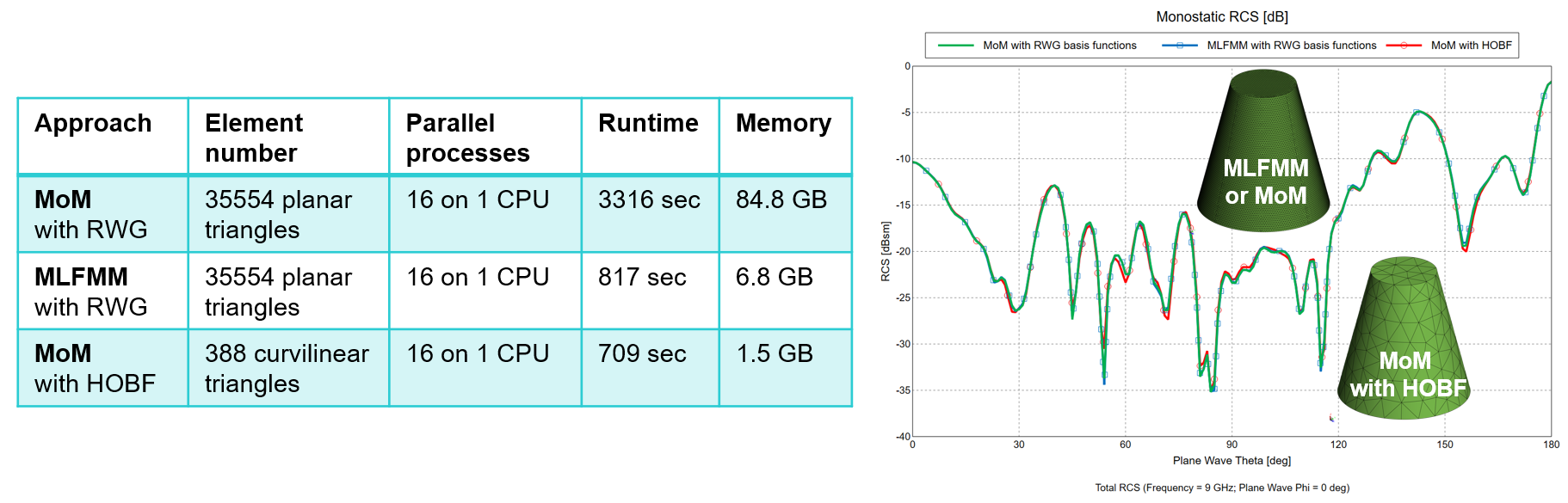
In principle HOBF can also be applied to MLFMM, but the advantages are less significant here than with MoM. For MLFMM it is recommended not to exceed element order 1.5 and to adjust the MLFMM box size to 0.4 wavelengths (instead of 0.25 wavelengths) as described in [4].
References:
- S. Rao, D. Wilton and A. Glisson, "Electromagnetic scattering by surfaces of arbitrary shape," in IEEE Transactions on Antennas and Propagation, vol. 30, no. 3, pp. 409-418, May 1982, doi: 10.1109/TAP.1982.1142818.
- J. van Tonder and U. Jakobus, "Introduction of curvilinear higher-order basis functions for MoM and MLFMM in FEKO," CEM'13 Computational Electromagnetics International Workshop, Izmir, Turkey, 2013, pp. 13-14, doi: 10.1109/CEM.2013.6617114.
- B. M. Notaros, "Higher Order Frequency-Domain Computational Electromagnetics," in IEEE Transactions on Antennas and Propagation, vol. 56, no. 8, pp. 2251-2276, Aug. 2008, doi: 10.1109/TAP.2008.926784.
- U. Jakobus and J. v. Tonder, Anwendung von Basisfunktionen höherer Ordnung auf gekrümmten Netzelementen zur beschleunigten Analyse von EMV-Problemen mit der Momentenmethode, EMV 2014, Düsseldorf.
- “EDA-workshop ‘Radar signatures & EM benchmarks’,” Nov. 2019. Available: https://www.fhr.fraunhofer.de/en/events/2019/eda-workshop-radar-signatures-and-em-benchmarks.html