Background
In aerodynamic design, particularly for aircraft with delta or highly swept wings, accurate lift prediction is not just a convenience; it’s a necessity. At high angles of attack, traditional linear lift models fail to capture a critical phenomenon: vortex lift. This blog post explores vortex lift correction, with a special focus on the Polhamus suction analogy, a widely referenced correction models in potential flow aerodynamics.
What is Vortex Lift?
Highly swept wings (aka Delta wings), especially those with sharp leading edges, tend to generate strong leading-edge vortices when flown at moderate to high angles of attack. These vortices create intense low-pressure zones over the upper wing surface, significantly increasing lift beyond what standard attached-flow theory would predict. This additional lift is termed vortex lift.
You’ll see this effect in aircraft like:
- The Concorde (slender delta wing)
- The F-16 Fighting Falcon
- Modern stealth fighters with faceted geometries
But while the lift goes up, so does drag. The key insight from Polhamus was that this extra lift, vortex lift, could be modelled not by computing exact vortex trajectories, but by borrowing a familiar aerodynamic concept: leading-edge suction.
Why Traditional Models Fail?
When it comes to predicting lift on sharp-edged delta wings at high angles of attack, traditional aerodynamic models fall short for two fundamental reasons:
- Assumption of Attached Flow
Most classical models, like thin airfoil theory and lifting-line theory are built on the assumption that airflow stays smoothly attached to the wing surface. This assumption breaks down completely for sharp-edged delta wings, where flow intentionally separates from the leading edge, forming large spiral vortices over the upper surface.
Instead of a clean stream of air accelerating over the top of the wing, the flow rolls up into coherent vortices that generate suction-like low-pressure zones. These vortices contribute significant lift, known as vortex lift, which cannot be captured by models that assume flow never separates.
- Inviscid and Irrotational Flow
Traditional models also assume inviscid (zero viscosity) and irrotational flow. However, vortex lift is a product of viscous interactions and rotational motion, air rotating around a vortex core. These phenomena are central to the formation and stability of the vortices that dominate delta wing aerodynamics at high angles of attack.
Since classical potential flow theory prohibits rotation and shear, it completely misses the physics of vortex creation. This makes it inherently incompatible with the flow structures that generate vortex lift.
The Polhamus Leading-Edge Suction Analogy
Instead of trying to model complex vortex geometry directly, Polhamus proposed that the force required to maintain the vortex was equivalent to the leading-edge suction force in potential flow, the same force that would be developed around a leading edge with attached flow.
The analogy worked like this:
- In potential flow, sharp leading edges produce suction peaks (negative pressure) that increase lift.
- In vortex flow, although the leading-edge suction is lost due to separation, a new form of lift arises, one that can be equated to the original suction force, just applied differently.
By rotating the theoretical suction force vector into the wing-normal direction, Polhamus developed a vortex lift term that could be added to the traditional lift model.
Polhamus’ model was developed for subsonic speeds and classic delta wings. At supersonic speeds, where shockwaves can interfere with vortex formation, the analogy weakens. The paper suggests that vortex lift diminishes as the leading edge falls behind the Mach line.
Polhamus Vortex Lift Correction Formulation
Altair FlightStream can calculate the forces induced by a potential flow over a lifting surface, the Polhamus correction method is used to estimate the additional component of lift over a delta wing, when a leading-edge vortex appears.
Using the Polhamus vortex lift correction, the total lift coefficient becomes:
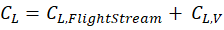
Where:
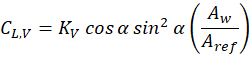
Here, \alpha is the angle of attack (in radians), Kv is the constant of proportionality in vortex lift equation, Aw is the wing area and Aref is the reference area.
Values of Kv have been calculated for a series of delta wings by using the lifting-surface theory as shown below.
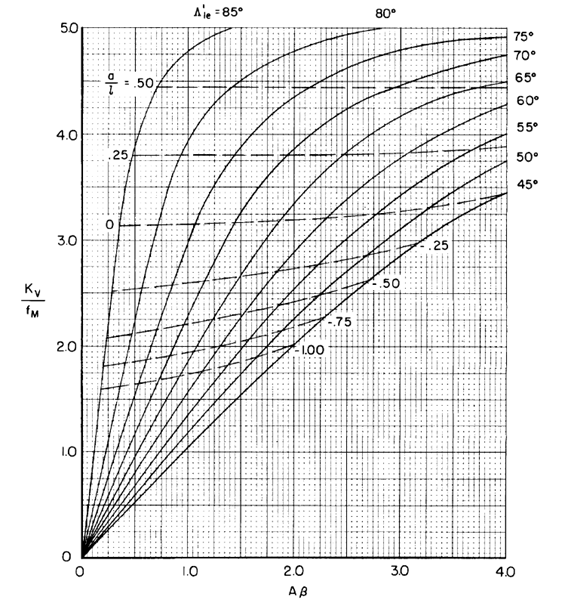
A Python-based script is included in this blog post to calculate the corresponding Kv value based on the input parameters: aspect ratio, sweep angle, and Mach number.
Additionally, the extra drag and pitching moment contributions resulting from vortex lift can be expressed as:
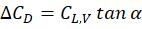
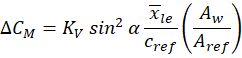
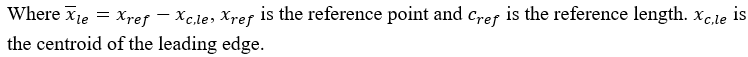
Key Parameters That Influence Vortex Lift
- Leading-edge sweep angle: More sweep leads to stronger vortices.
- Angle of attack: Vortex lift becomes significant at moderate to high angle of attack.
- Wing sharpness and shape: Sharper leading edges trigger earlier vortex formation.
- Reynolds number: Affects vortex stability and behaviour (effect captured through Mach number).
Applications and Importance
Accurate modelling of vortex lift is essential for:
- Designing high-performance aircraft that rely on vortex lift for enhanced manoeuvrability and delayed stall.
- Simulating flight performance of unmanned aerial vehicles (UAVs), particularly those with unconventional planforms.
- Stability and control analysis, where vortex lift can significantly shift aerodynamic centre.
Example
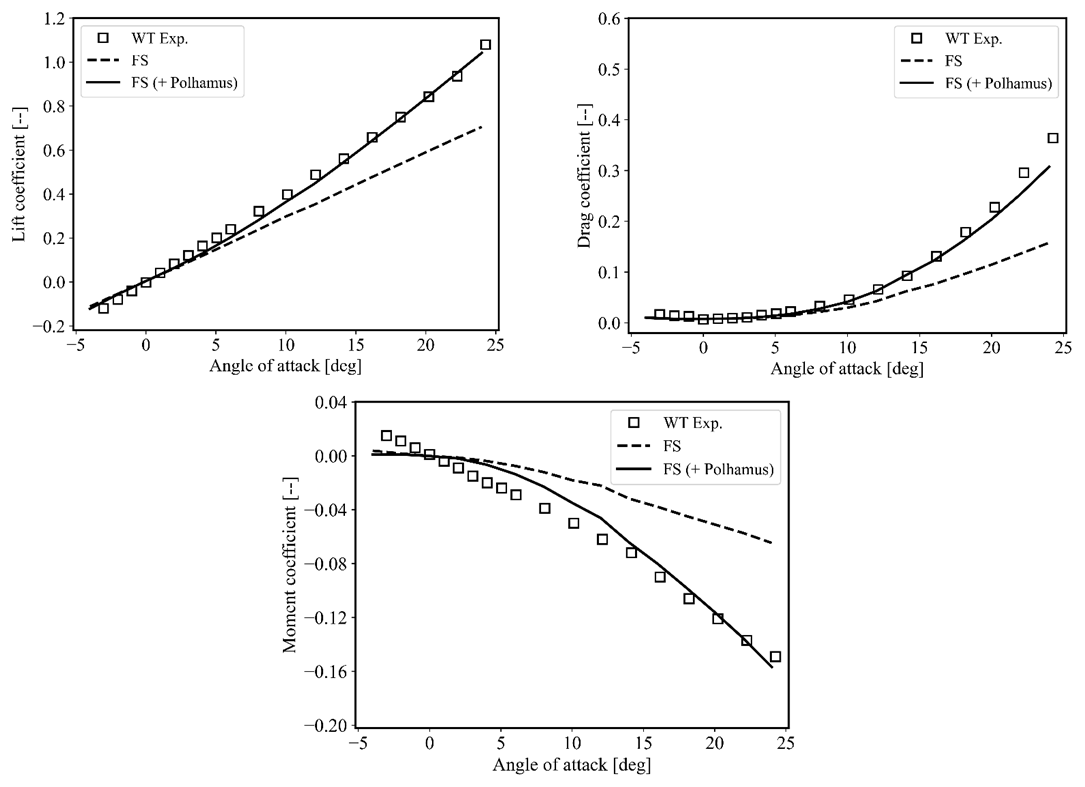
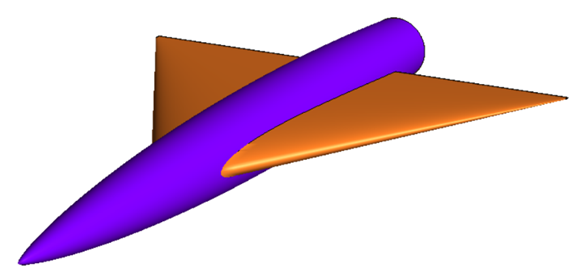
Altair FlightStream is used to simulate a delta wing-body geometry shown below.
The figures below compare the aerodynamic coefficients predicted by Altair FlightStream with wind tunnel data at a Mach number of 0.24 and a Reynolds number of 3 million. As shown, applying the Polhamus correction yields good agreement with the experimental results.