How averaging errors can be both useful and deceiving
Altair Employee
As CAE engineers we are used to the mindset of questioning model accuracy. Can your finite element model capture the physics of the event it's meant to model? This is probably why the most frequent question I get when engineers build machine learning models is "How accurate is the model?".
A common way of showing accuracy for regression models is to use the coefficient of determination, or r2 (see Determining the Root of R-squared) on a validation set that the model has not previously seen. R2 is a value ranging from -Infinity to 1.0 where 1.0 is the best possible score and as it approaches zero (or falls below zero) the model is not fit for purpose. The fact that it is dimensionless makes it intuitive to work with. But what happens when the model is not predicting a scalar quantity?
In this post we will look closer at real time predictions of complete simulation results. This is a feature available in HyperWorks Design Explorer. The figure below shows such a prediction of the plastic strain contour. Let's discuss whether this prediction can be trusted.
When zooming in (right picture) we can see that plastic strain values are predicted at each element centroid. The predicted plastic strain of the two marked elements are 0.133 and 0.127 with corresponding r2 values of 0.92 and 0.87 respectively. Of course, we could do this for all the elements but even for this, relatively small (6930 elements) model it can become a bit tedious.
One option is to calculate an average of the r2 over all the elements. This gives us an average r2 of -14.3. Wait... I'll calculate that again.... yes, that is correct.... Were we just lucky when we selected those two elements with high r2 before? Is the rest of the prediction bad? Let's dig a bit deeper.
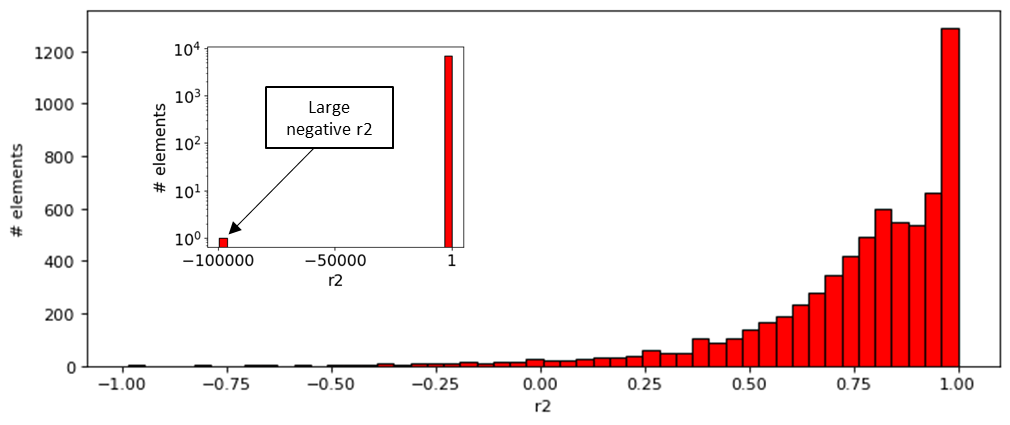
Looking at the histogram below of the distribution of r2 values for the elements, we can see (in the small diagram), that there is a small number of large negative r2 values. Looking at the rest of the values (big diagram) we can see that most of the r2 values are good, really good in fact. 85% of the elements have an r2 of 0.5 or higher and 60% of the elements have an r2 of 0.75 or higher.
Let's look at these negative values in the table below. Te table is presented in order of increasing r2 with the variance and mean average error (MAE) presented as well. There's a number of large negative r2 values that seem to be the culprit in skewing our average r2 to be negative. We also observe that although the mean average error (MAE) for all elements stay fairly constant the variance, for each of the elements with negative r2, is approaching zero. The elements with variance close to zero are hardly affected by the design variables. We therefore expect the result to always be the same and any deviation (however small) is large compared to the variance and leads to a huge negative r2.
This means that an average r2 is not a very good metric to use for predicting entire simulation results in this way. So how do we convey that our predictive model is in fact accurate? Below are what we have been experimenting with.
Average Mean absolute error (AMAE) = 0.0023
AMAE is an average of the mean average error (MAE) of all elements. The value is relatable as it is in the same unit as the result type. In this case the maximum plastic strain is 0.6 so the AMAE is quite low in comparison.
Weighted average r2 = 0.8
Weighing the r2 values by the variance (Large variance means large weight and vice versa) leads to a metric that puts little importance to elements with low variance and more to elements with larger variance. A benefit compared to AMAE is that it's dimensionless and is therefore easier to relate to and compare to predictive models of other result types.
Average errors contoured
Finally, why not visualize the average error of each element on the model? That way we can see in what areas we can expect our largest errors to be.
These are some examples of endless possibilities in conveying model accuracy. What information would you like to see for models you have built?