Hello everyone
As a part of some simulations I am running, I tried to simulate a 2-ray path model in ProMan. To achieve this I approximated a PEC in WallMan ( εr =1 (lowest possible), µr = 1, σ = 6e+006 (highest possible)) as a floor plate. In ProMan I simulated an antenna at one end (height 4.5m) and I plotted the received power vs the distance at height 4.5m. Everything about this graph is correct, the locations of the oscillations are exactly where I would suspect them theoretically and once Δ R drops below λ /2 the oscillations stop and I get a constant slope. However due to the small incidence angle and the relative height of the transmitter and respective receiver, I would predict the path loss of this slope to be 4 (40 dB/decade decrease, which I should get regardless of material properties because the angle is so small and I only have the direct ray and the reflected ray). But I never get this value from the simulations. The lower I place my transmitter, the lower the path loss gets. The path loss from every simulation has been lower then the expected value. Does anyone know the reason for this deviation or is someone struggling with the same phenomena?
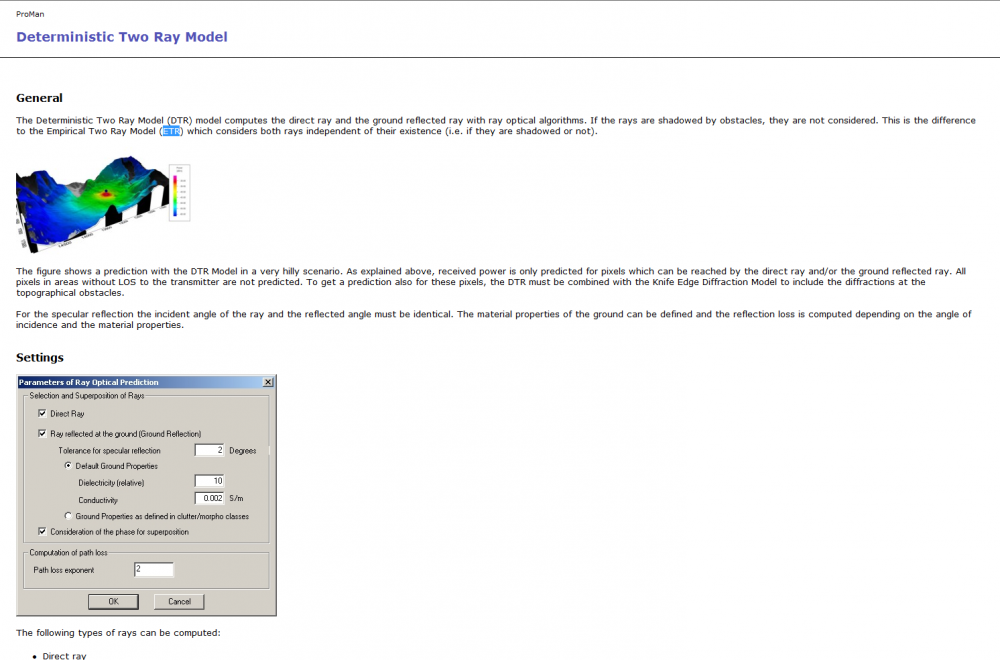
I tried to look for an answer in the manual and found a possible cause for my mismatch. I suspect that my tolerance for the angle of incidence is to low. Therefore ProMan has trouble correctly interfering these two rays. I found a page in the manual, from which I have included a print screen, where oen could adjust this value. However I haven't been able to locate this menu for my simulations.
Thanks in advance!
Kind regards
Publi
<?xml version="1.0" encoding="UTF-8"?>