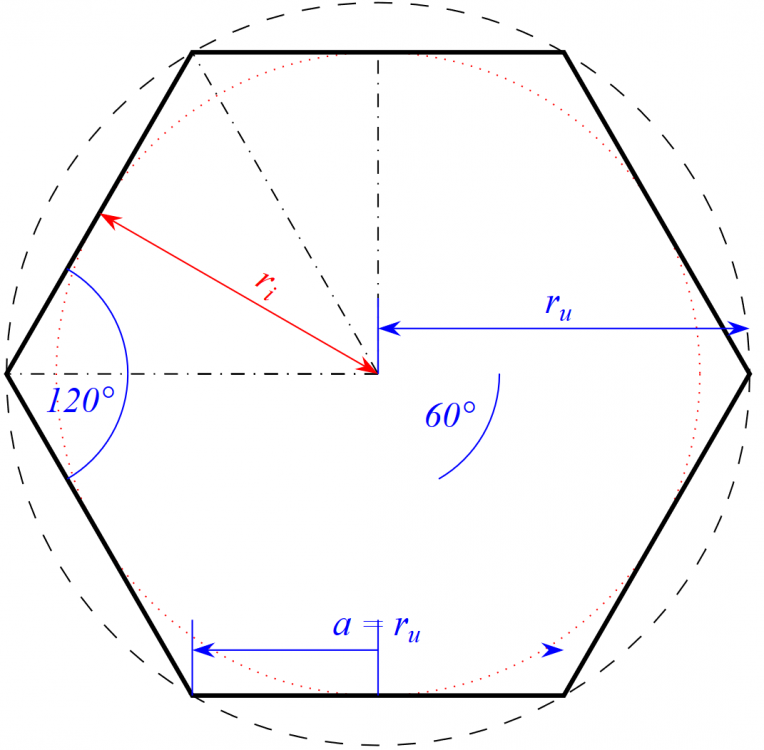
Dispersion Diagram of a Unit Cell of a Periodic Structure
Answers
-
Hi Professor Hussain Al-Rizzo,
I will try to set up a FEKO model for you.
0 -
Hi Dr. Torben,
Thank you for your kind response. I will run the model an update you,
Best regards
0 -
Hi Dr. Torben,
Thank you for your kind reply. I ran the model, however, the problem that I am seeking is an eignevalue problem and the geometry is not the FSS you have used. The geometry is a grounded substrate with a via and conducting patch on top. Then the natural modes are usually found from an eigen mode solver after adding an air layer and PML. There is a lengthy procedure to follow by varying the phase among three periodic axes called Brillouin zone (from solid state physics). The final results are represented by a dispersion diagram frequency versus phase for a number (usually three) for TM and TE modes. I have searched the literature on FEKO and dispersion diagram and did not find results reported using FEKO. Currently, Lumerical, CST (application note attached), and HFSS have separate eignemode solver to perform such calculations.
Therefore, I wonder if you can solve this problem using FEKO?
Thank you and best regards
0 -
Hello Professor Hussain Al-Rizzo,
I was only concentrating on the creation of the infinite structure like shown in
Regarding the option of dispersion diagrams of infinite (Periodic Boundary Condition) structures in FEKO, there is a feature request under discussion. This feature request was originally started from an email from you to FEKO Support in November 2012
/emoticons/default_smile.png' srcset='/emoticons/smile@2x.png 2x' title=':)' width='20' /> I will in any case keep you updated if there are good news for you.
0 -
Dear Dr. Voigt,
Thank you for your kind reply. I entered history in FEKO since 2012, I forgot that e mail. Adding this option will be an exceptional addition to the value of FEKO in the metamaterial world. Thank you and best regard.
0


 <?xml version="1.0" encoding="UTF-8"?>
<?xml version="1.0" encoding="UTF-8"?>