How clustering can help build expert knowledge into optimisation

Jonathan Ollar_21112

During my doctorate, my supervisor used to repeat the mantra “The most important thing in optimization is problem formulation” and although I trusted him, I didn't realize how right he was. Some things you must learn the hard way – And I did. I have spent countless hours re-running structural optimizations only because I hadn't defined the requirements of the problem properly. Many times, the reason for this was my inability to express the desired outcome in terms that the optimizer would understand.

Using automotive crashworthiness as an example, engineers will usually try to achieve a specific deformation mode, such as axial crushing. Even if one can find a solution that satisfies the safety targets but does not conform to the desired deformation mode, it's likely to be discarded.

So how would we go about defining deformed shape as a requirement? One option that I have used many times, with mixed success, is constraining the displacement of various points on the structure. Although this can work well, it is not trivial to decide which points to use nor their allowed displacement. It takes significant effort defining these - and likely re-running the optimization a few times to get it right.

Let me suggest an alternative approach using machine learning.

  

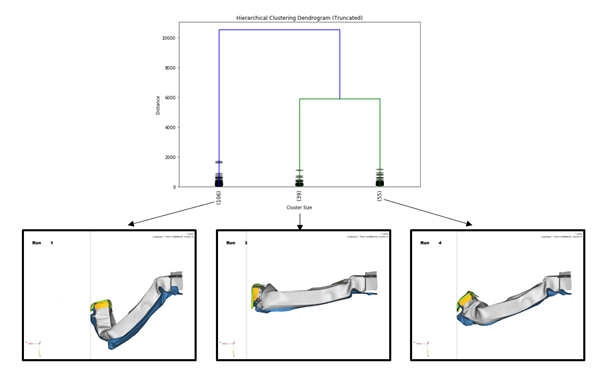
In this example, we are designing a front crash rail that we would like to deform axially. The structure has a number of designable parameters, both shape and thickness. As ever, when talking about Machine learning, we need data, so we run a design of experiments (DOE) using a space filling DOE, such as MELS, in HyperStudy. Next, we are going to make use of Clustering, which is an unsupervised Machine Learning method that groups records (in our case, DOE runs) together based on their similarity. Similarity is an ambiguous term (it could be colour, shape, size, etc.), so we must decide what similarity means to us. In our case, we use the (Euclidean) distance between displacement vectors as our measure of similarity.

Once this is defined, we let the clustering algorithm find groups (or clusters). As you can see in the picture, we are presented with three clusters, each with a different deformation shape. In each of the three groups, there are a number of runs that conform to the shape you can see in the picture.

What if I told you that you could now decide which cluster you prefer, and the optimization algorithm makes sure that the design conforms to this cluster? This is functionality we are building. If you are interested in seeing an example of its use, check out this video.

Please comment on whether this technology could help you in your work.