How to morph an arc with keeping the tangency and symmetry constraints?
Hi, everyone.
I encountered a problem when morphing an arc. The arc cannot keep the tangency on symmetry plane when altering the radius of the arc (shown in figure). How to keep the vertical tangential direction on point B and D while morphing?
<?xml version="1.0" encoding="UTF-8"?>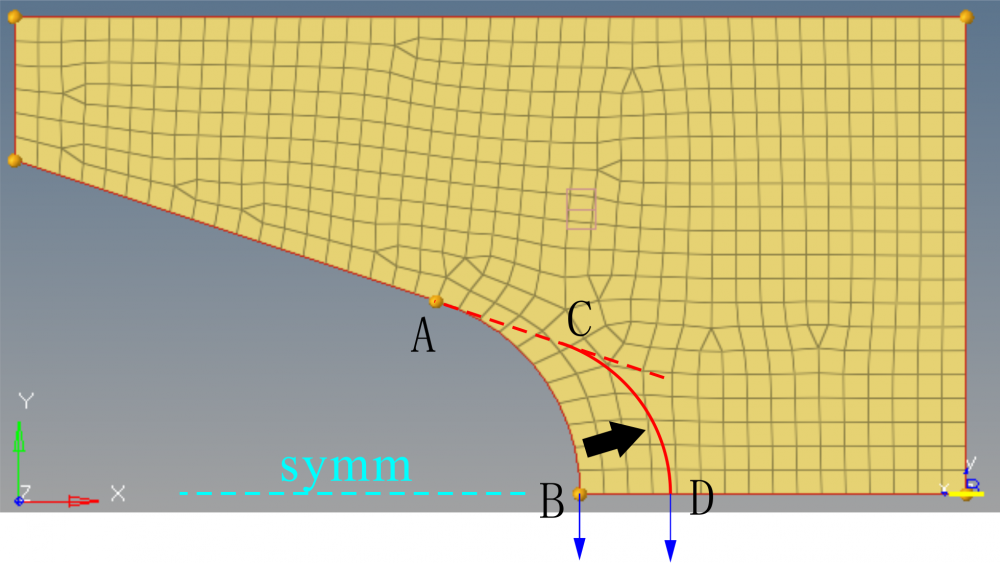
Thanks.
Answers
-
Can't this constraint be achieved in HyperMorph?
0 -
i have only one idea.
you should create line B and project to surface.
after you will remesh and delete extra face.
0 -
0
-
i can't do it by morph tool=(
0 -
Hi, Mrt
I tried this test by morph tools many times. I found that, in 'alter dimensions' subpanel, we can only use the 'fillet' approach to keep the tangency of arc AB at point A, but the symmetry of this arc has no way to be constrained by assign tangent vector.
If do this test in whole model, I guess this problem could be solved easily, because the constraint of the symmetry of the arc does not existed anymore. But if the geometry model is huge and complex, the symmetry constraint in half model like this problem is still nesscessary.
Your idea, do it like HM-3530 by map to geometry, is still worth to try. I will try it.
Many thanks.
0 -
Hi,
First, you draw the final profile ACD,
From menu Morph>Free hand:
1) Morph B to D
==>
2) Enter panel F7>remap
remap below misaligned nodes:
<?xml version="1.0" encoding="UTF-8"?>
3) Enter panel smooth to adjust mesh lines
<?xml version="1.0" encoding="UTF-8"?>
==> Is this OK for you?
0 -
Hi, tinh
The purpose of this test is to get an shape variable which is able to be used in optimization. Your advised method is based on the pre-establised arc. The constraints of the symmetry and tangency are ensured by creating the new arc manually. I'm looking for a simple and direct method to establish the relationship between the designable shape variable and the radius of this arc.
Many thanks.
0 -
HI Mansin,
You can try Tinh's method by using pre-established arc. In order to get your shape variable for optimization, you can use the Map to Geom tool in morphing with Fit to Line option as shown below instead of using F7-remap tool. Then go to Morph panel to save your shape
<?xml version="1.0" encoding="UTF-8"?>
To get more shape with different radius for the arc, you can try the apply shape subpanel, apply the shape you saved but with a different multiplier (eg:0.1). The shape will change gradually and you can save shape to get more shapes for your optimization. The following video is an example;
0 -
Hi, Toan Nguyen
If I apply the shape with different multiplier, the obtained intermediate curve is not an arc, actually it is an interpolated curve, just like this:
Many thanks.
0 -
hi Masin,
In that case, I think you have to repeat the process with several pre-defined arcs
0
Altair Employee
